高中数学原根与指数试题

已知函数f(x)=4^x+m·2^x+1有且仅有一个零点,求m的取值范围,并求出该零点.

设f（x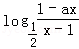）=为奇函数，a为常数．
（1）求a的值；
（2）判断f（x）在区间（1，+∞）上的单调性，并证明你的结论；
（3）若对于区间（3，4）上的每一个x的值，不等式f（x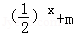）＞恒成立，
求实数m的取值范围．

设函数，则满足的的取值范围（     ）

A．

B．

C．

D．

函数的图象大致是（ ）

若函数y=()^|1-x|+m的图象与x轴有公共点,则m的取值范围是(　　)

A．m≤-1	B．m≥1
C．-1≤m<0	D．0<m≤1

已知函数，.
（1）若函数在上不具有单调性，求实数的取值范围；
（2）若.
（ⅰ）求实数的值；
（ⅱ）设，，，当时，试比较，，的大小．

若，，，则当x>1时，a,b,c的大小关系是（  ）

A．

B．

C．

D．

已知函数f(x)＝若关于x的方程f(f(x))＝0有且仅有一个实数解，则实数a的取值范围是(　　)

A．(－∞，0)	B．(－∞，0)∪(0,1)
C．(0,1)	D．(0,1)∪(1，＋∞)

已知函数f(x)＝
(1)若x<a时，f(x)<1恒成立，求a的取值范围；
(2)若a≥－4时，函数f(x)在实数集R上有最小值，求实数a的取值范围．

设a＝2 011^0.1，b＝ln，c＝log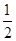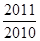，则a，b，c的大小关系是________．

已知函数 ，函数.
（1）求函数与的解析式,并求出，的定义域;
（2）设，试求函数的最值.

设函数，若对任意给定的，都存在唯一的，满足，则正实数的最小值是（   ）

A．

B．

C．2

D．4

已知函数（为常数），函数定义为：对每一个给定的实数，
（1）求证：当满足条件时，对于,；
（2）设是两个实数，满足，且，若，求函数在区间上的单调递增区间的长度之和.（闭区间的长度定义为）

定义在R上的函数满足，，且时， 则       .

设则的大小关系是 （  ）

A．

B．

C．

D．