高中数学二次剩余试题

已知函数f(x)＝x²－2(a＋2)x＋a²，g(x)＝－x²＋2(a－2)x－a²＋8.设H₁(x)＝max{f(x)，g(x)}，H₂(x)＝min{f(x)，g(x)}(max{p，q}表示p，q中的较大值，min{p，q}表示p，q中的较小值)．记H₁(x)的最小值为A，H₂(x)的最大值为B，则A－B＝(　　)

A．a^2－2a－16

B．a^2＋2a－16

C．－16

D．16

若在区间(-∞，1]上递减，则a的取值范围为(    )

A．[1，2)

B．[1，2]

C．[1,+∞)

D．[2，+∞)

已知直线y＝mx与函数的图象恰好有3个不同的公共点，则实数m的取值范围是（   ）

A．(，4)

B．(，＋∞)

C．(，5)

D．(，)

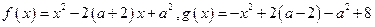已知函数．设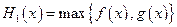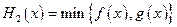， (max{p，q}表示p，q中的较大值，min{p，q}表示p，q中的较小值)．记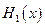的最小值为A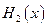，的最大值为B，则(    )

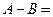A．16

B．

C．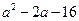

D．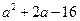

若一元二次不等式对一切实数都成立，则的取值范围为（  ）

A．

B．

C．

D．

设二次函数满足条件：①；②函数的图像与直线相切．
（1）求函数的解析式；
（2）若不等式在时恒成立，求实数的取值范围．

在直角坐标系中，曲线C₁的参数方程为：（为参数），以原点为极点，x轴的正半轴为极轴，并取与直角坐标系相同的长度单位，建立极坐标系，曲线C₂是极坐标方程为：，
（1）求曲线C₂的直角坐标方程；
（2）若P，Q分别是曲线C₁和C₂上的任意一点，求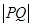的最小值.

椭圆c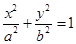：（a>b>0）的离心率为，过其右焦点F与长轴垂直的弦长为1，
（1）求椭圆C的方程；
（2）设椭圆C的左右顶点分别为A，B，点P是直线x=1上的动点，直线PA与椭圆的另一个交点为M，直线PB与椭圆的另一个交点为N，求证：直线MN经过一定点.

已知
（1）设，求的最大值与最小值；
（2）求的最大值与最小值；

已知函数，.
（1）若函数在上不具有单调性，求实数的取值范围；
（2）若.
（ⅰ）求实数的值；
（ⅱ）设，，，当时，试比较，，的大小．

对于任意a∈[-1,1],函数f(x)=x²+(a-4)x+4-2a的值恒大于零,那么x的取值范围是(　　)

A．(1,3)	B．(-∞,1)∪(3,+∞)
C．(1,2)	D．(3,+∞)

已知函数f(x)＝
(1)若x<a时，f(x)<1恒成立，求a的取值范围；
(2)若a≥－4时，函数f(x)在实数集R上有最小值，求实数a的取值范围．

设函数f(x)＝ax－(1＋a²)x²，其中a>0，区间I＝{x|f(x)>0}．
(1)求I的长度(注：区间(α，β)的长度定义为β－α)；
(2)给定常数k∈(0，1)，当1－k≤a≤1＋k时，求I的长度的最小值．

若关于x的不等式2－x²≥|x－a|至少有一个正数解，则实数a的取值范围是________．

一次函数是上的增函数，,已知.
（1）求；
（2）若在单调递增，求实数的取值范围；
（3）当时，有最大值，求实数的值.