高中数学二次剩余解答题

设函数．
（I）当时，求函数的定义域；
（II）若函数的定义域为，试求的取值范围

已知二次函数的图像关于直线对称，且在轴上截得的线段长为2．若的最小值为，求：
（1）函数的解析式；
（2）函数在上的最小值．

已知向量，，其中.函数在区间上有最大值为4,设.
(1)求实数的值；
(2)若不等式在上恒成立，求实数的取值范围.

已知函数是偶函数。
（1）求的值；
（2）设函数，其中实数。若函数与的图象有且只有一个交点，求实数的取值范围。

已知二次函数f(x)=ax²+bx,f(x+1)为偶函数,函数f(x)的图象与直线y=x相切.
（I）求f(x)的解析式;
（II）已知k的取值范围为[,+∞),则是否存在区间[m,n](m<n),使得f(x)在区间[m,n]上的值域恰好为[km,kn]?若存在,请求出区间[m,n];若不存在,请说明理由.

已知二次函数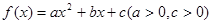满足条件，及．
（1）求的解析式；
（2）求在上的最值．

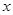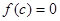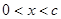已知二次函数的图像与轴有两个不同的公共点，且有，当时，恒有、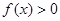
（1）试比较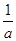与c的大小；
（2）试求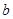的取值范围；
（3）若以二次函数的图像与坐标轴的三个交点为顶点的三角形的面积为5，求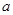的取值范围

销售甲、乙两种商品所得利润分别是P(万元)和Q(万元)，它们与投入资金t(万元)的关系有经验公式P＝，Q＝t．今将3万元资金投入经营甲、乙两种商品，其中对甲种商品投资x(万元)．
求：(1)经营甲、乙两种商品的总利润y(万元)关于x的函数表达式；
(2)总利润y的最大值．

“地沟油”严重危害了人民群众的身体健康，某企业在政府部门的支持下，进行技术攻关，新上了一种从“食品残渣”中提炼出生物柴油的项目，经测算，该项目月处理成本y(元)与月处理量x(吨)之间的函数关系可以近似的表示为：

且每处理一吨“食品残渣”，可得到能利用的生物柴油价值为200元，若该项目不获利，政府将补贴.
(1)当x∈[200,300]时，判断该项目能否获利？如果获利，求出最大利润；如果不获利，则政府每月至少需要补贴多少元才能使该项目不亏损；
(2)该项目每月处理量为多少吨时，才能使每吨的平均处理成本最低？

(本小题满分14分) 如图，已知抛物线与坐标轴分别交于A、B、C三点，过坐标原点O的直线与抛物线交于M、N两点.分别过点C、D作平行于轴的直线、.（1）求抛物线对应的二次函数的解析式；（2）求证:以ON为直径的圆与直线相切；（3）求线段MN的长（用表示），并证明M、N两点到直线的距离之和等于线段MN的长.

已知关于x的一元二次函数
(1)设集合P={1，2，3}和Q={－1，1，2，3，4}，分别从集合P和Q中随机取一个数作为和，
求函数在区间[上是增函数的概率；
(2)设点（，）是区域内的随机点，求函数上是增函数的概率.

已知函数（为实数， ，）．
（1）若函数的图象过点，且方程有且只有一个根，求的表达式；
（2）在（1）的条件下，当时，是单调函数，求实数的取值范围．

（本小题满分13分）
已知函数,设函数，
（1）若，且函数的值域为，求的表达式.
（2）若在上是单调函数，求实数的取值范围.

(本小题满分12分)  已知函数f(x)＝
(1)作出函数的图像简图，并指出函数的单调区间；
（2）若f(2－a²)>f(a)，求实数a的取值范围.

二次函数f(x)满足f(x+1)-f(x)=2x,且f(0)=1.
（1）求f(x)的解析式；
（2）在区间[－1，1]上，y=f(x)的图象恒在y=2x+m的图象上方，求实数m的取值范围