函数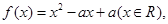 数列
数列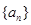 的前
的前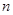 项和
项和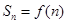 ,且
,且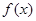 同时满足:①不等式
同时满足:①不等式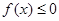 的解集有且只有一个元素;②在定义域内存在
的解集有且只有一个元素;②在定义域内存在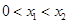 ,使得不等式
,使得不等式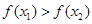 成立.
成立.
(1)求函数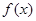 的表达式;
的表达式;
(2)求数列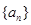 的通项公式.
的通项公式.
“地沟油”严重危害了人民群众的身体健康,某企业在政府部门的支持下,进行技术攻关,新上了一种从“食品残渣”中提炼出生物柴油的项目,经测算,该项目月处理成本y(元)与月处理量x(吨)之间的函数关系可以近似的表示为:
且每处理一吨“食品残渣”,可得到能利用的生物柴油价值为200元,若该项目不获利,政府将补贴.
(1)当x∈[200,300]时,判断该项目能否获利?如果获利,求出最大利润;如果不获利,则政府每月至少需要补贴多少元才能使该项目不亏损;
(2)该项目每月处理量为多少吨时,才能使每吨的平均处理成本最低?
(本小题14分)已知函数 是定义在R上的偶函数,且当
是定义在R上的偶函数,且当 ≤0时,
≤0时,
 .
.
(1)求出 的解析式;
的解析式;
(2)现已画出函数 在y轴左侧的图像,如图所示,请补出完整函数
在y轴左侧的图像,如图所示,请补出完整函数 的图像,并根据图像写出函数
的图像,并根据图像写出函数 的增区间和值域。
的增区间和值域。
某种商品在 天内每件的销售价格
天内每件的销售价格 (元)与时间
(元)与时间 (天)的函数关系用如图表示,该商品在
(天)的函数关系用如图表示,该商品在 天内日销售量
天内日销售量 (件)与时间
(件)与时间 (天)之间的关系如下表:
(天)之间的关系如下表:

(1)根据提供的图象(如图),写出该商品每件的销售价格 与时间
与时间 的函数关系式;
的函数关系式;
(2)根据表 提供的数据,写出日销售量
提供的数据,写出日销售量 与时间
与时间 的一次函数关系式;
的一次函数关系式;
(3)求该商品的日销售金额的最大值,并指出日销售金额最大的一天是 天中的第几天.(日销售金额
天中的第几天.(日销售金额 每件的销售价格
每件的销售价格 日销售量)
日销售量)
已知中心在原点,焦点在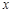 轴上的椭圆
轴上的椭圆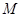 的离心率为
的离心率为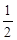 ,椭圆上异于长轴顶点的任意点
,椭圆上异于长轴顶点的任意点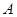 与左右两焦点
与左右两焦点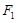 、
、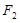 构成的三角形中面积的最大值为
构成的三角形中面积的最大值为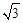 .
.
(1)求椭圆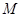 的标准方程;
的标准方程;
(2)已知点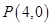 ,连接
,连接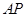 与椭圆的另一交点记为
与椭圆的另一交点记为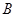 ,若
,若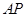 与椭圆相切时
与椭圆相切时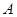 、
、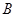 不重合,连接
不重合,连接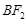 与椭圆的另一交点记为
与椭圆的另一交点记为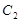 ,求
,求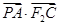 的取值范围.
的取值范围.
已知定义在区间[0,2]上的两个函数f(x)和g(x),其中f(x)=-x2+2ax+1+a2,g(x)=x- +
+ .
.
(1)求函数f(x)的最小值.
(2)对于∀x1,x2∈[0,2],f(x1)>g(x2)恒成立,求实数a的取值范围.
已知二次函数 .
.
(Ⅰ)若 ,且
,且 在
在 上单调递增,求实数
上单调递增,求实数 的取值范围;
的取值范围;
(Ⅱ)当 时,有
时,有 .若对于任意的实数
.若对于任意的实数 ,存在最大的实数
,存在最大的实数 ,使得当
,使得当 时,
时, 恒成立,试求用
恒成立,试求用 表示
表示 的表达式.
的表达式.
试题篮
()