高中数学二次剩余解答题

（本小题满分12分）定义在实数R上的函数y= f（x）是偶函数，当x≥0时，.
（Ⅰ）求f（x）在R上的表达式；
（Ⅱ）求y=f（x）的最大值，并写出f（x）在R上的单调区间（不必证明）.

（本小题满分12分）已知二次函数的图象过点（0，—3），且的解集（1，3）。
（1）求的解析式；
（2）若当时，恒有求实数t的取值范围。

已知二次函数的最小值为1，且。
（1）求的解析式；  
（2）若在区间上不单调，求实数的取值范围；
（3）在区间上，的图象恒在的图象上方，试确定实数的取值范围。

是否存在常数，使得函数在闭区间上的最大值为1？若存在，求出对应的值；若不存在，说明理由．

(本小题满分14分)已知，
1)若，求方程的解；
2)若对在上有两个零点,求的取值范围.

已知二次函数满足，，求的取值范围。

（本小题满分12分）已知二次函数f（x）满足：函数f（x+1）为偶函数，f（x）的最小值为-4，函数f（x）的图象与x轴交点为A、B，且AB=4，求二次函数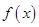的解析式．

(本小题满分12分)
已知二次函数, 满足且的最小值是．（Ⅰ）求的解析式；（Ⅱ）设函数，若函数在区间上是单调函数，求实数的取值范围。

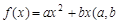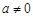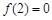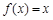已知二次函数为常数，且）满足条件：，且方程有两个相等的实数根．
（1）求的解析式；
（2）求函数在区间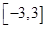上的最大值和最小值；
（3）是否存在实数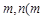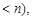使的定义域和值域分别为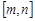和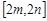，如果存在，求出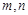的值，如不存在，请说明理由．

（本题12分）设二次函数，若的解集为，函数，（1）求与的值；（2）

已知二次函数
(1) 画出函数图像
（2）指出图像的开口方向、对称轴方程、顶点坐标；
（3）求函数的最大值或最小值；
（4）写出函数的单调区间

设二次函数满足下列条件：
①当时, 的最小值为0，且恒成立；
②当时，恒成立．
（I）求的值；
（Ⅱ）求的解析式；
（Ⅲ）求最大的实数m（m>1），使得存在实数t，只要当时，就有成立

已知x₁、x₂是关于x的一元二次方程x²+（3a-1）x+2a²-1=0的两个实数根，使得
（3x₁-x₂）（x₁-3x₂）=-80成立．求实数a的所有可能值．

已知二次函数，满足，且方程有两个相等的实根．
（1）求函数的解析式；
（2）当时，求函数的最小值的表达式．

已知二次函数的导函数的图像与直线平行，且在处取得极小值．设．
（1）若曲线上的点到点的距离的最小值为，求的值；
（2）如何取值时，函数存在零点，并求出零点．