高中数学二次剩余试题

已知函数，若|f(x)|≥ax，则a的取值范围是（    ）

A．(－∞，0]	B．(－∞，1]
C．[－2,1]	D．[－2,0]

已知直线y＝mx与函数的图象恰好有3个不同的公共点，则实数m的取值范围是（   ）

A．(，4)

B．(，＋∞)

C．(，5)

D．(，)

已知上恒成立，则实数a的取值范围是（   ）

A．

B．

C．

D．

若函数 的定义域为R，则a的取值范围是(   )

A．

B．

C．

D．

已知函数，若，则实数（   ）

A．

B．

C．2

D．9

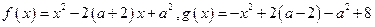已知函数．设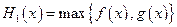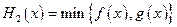， (max{p，q}表示p，q中的较大值，min{p，q}表示p，q中的较小值)．记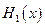的最小值为A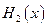，的最大值为B，则(    )

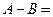A．16

B．

C．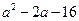

D．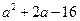

若一元二次不等式对一切实数都成立，则的取值范围为（  ）

A．

B．

C．

D．

函数（）的最大值等于         .

设二次函数满足条件：①；②函数的图像与直线相切．
（1）求函数的解析式；
（2）若不等式在时恒成立，求实数的取值范围．

不等式a²+8b²≥λb（a+b）对于任意的a，b∈R恒成立，则实数λ的取值范围为

在直角坐标系中，曲线C₁的参数方程为：（为参数），以原点为极点，x轴的正半轴为极轴，并取与直角坐标系相同的长度单位，建立极坐标系，曲线C₂是极坐标方程为：，
（1）求曲线C₂的直角坐标方程；
（2）若P，Q分别是曲线C₁和C₂上的任意一点，求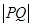的最小值.

椭圆c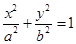：（a>b>0）的离心率为，过其右焦点F与长轴垂直的弦长为1，
（1）求椭圆C的方程；
（2）设椭圆C的左右顶点分别为A，B，点P是直线x=1上的动点，直线PA与椭圆的另一个交点为M，直线PB与椭圆的另一个交点为N，求证：直线MN经过一定点.

设max{f(x)，g(x)}=,若函数n(x)=x²+px+q(p，q∈R)的图象经过不同的两点（，0）、（，0），且存在整数n使得n<<<n+1成立，则（    ）

A．max{n(n),n(n+1)}>1	B．max{n(n),n(n+1)}<1
C．max{n(n),n(n+1)}>	D．max{n(n),n(n+1)}>

若且,则函数与函数在同一坐标系内的图像可能是(   )

某通讯公司需要在三角形地带区域内建造甲、乙两种通信信号加强中转站，甲中转站建在区域内，乙中转站建在区域内．分界线固定，且=百米，边界线始终过点，边界线满足．
设()百米，百米.

(1)试将表示成的函数，并求出函数的解析式；
(2)当取何值时？整个中转站的占地面积最小，并求出其面积的最小值．