高中数学二次剩余试题

（本小题满分14分）
已知函数，，且对恒成立．
（1）求a、b的值；
（2）若对，不等式恒成立，求实数m的取值范围．
（3）记，那么当时，是否存在区间（），使得函数在区间上的值域恰好为？若存在，请求出区间；若不存在，请说明理由．

若与在区间上都是减函数，则a的取值范围是（）
A．              B．              C．           D．
8．求下列函数的零点，可以采用二分法的是（ B ）
A．                                                 B．
C．                                      D．

【文】已知二次函数，若对于任意实数x，有的最小值为          。

（本小题满分12分）
已知函数，
（Ⅰ）设两曲线与有公共点，且在公共点处的切线相同，若，试建立关于的函数关系式；
（Ⅱ）若在（0，4）上为单调函数，求的取值范围．

点在函数的图象上，点与点关于轴对称,且在直线上，则函数在区间上           （   ）

A．既没有最大值也没有最小值	B．最小值为-3，无最大值
C．最小值为-3，最大值为9	D．最小值为，无最大值

已知函数，关于的方程，若方程恰有8个不同的实根，则实数k的取值范围是               .

(本题满分12分)
已知二次函数满足且．
（Ⅰ）求的解析式；
（Ⅱ）当时，不等式：恒成立，求实数的范围．

（本小题满分14分）
已知二次函数(为常数).
（1）若函数是偶函数，求的值；
（2）若，求函数的最小值；
（3）在(1)的条件下, 满足的任意正实数，都有，求实数的取值范围。

函数y="2x" -的图像大致是 （     ）                                          

函数在区间上有最小值，则函数在区间上一定（  ）

A．有最小值

B．有最大值

C．是减函数

D．是增函数

函数y＝x2－2x在区间[a，b]上的值域是[－1，3]，

则点(a，b)的轨迹是图中的

A．线段AB和线段AD	B．线段AB和线段CD
C．线段AD和线段BC	D．线段AC和线段BD

（本小题满分12分）
设函数．
（Ⅰ）求的最小值；
（Ⅱ）若对恒成立，求实数的取值范围．

(本题满分12分)
已知函数，
⑴ 求函数的最大值关于的解析式
⑵ 画出的草图，并求函数的最小值.

若二次函数在区间上为减函数，那么（  ）

A．

B．

C．

D．

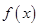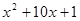已知函数=，则函数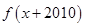的最小值及对称轴方程分别为（    ）

A．-24，-2015

B．24，x=“-2015”

C．24，x=“2015”

D．-24，x=-2015