高中数学二次剩余试题

已知在区间上是增函数.
（1）求实数的值组成的集合；
（2）设关于的方程的两个非零实根为、．试问：是否存在实数，使得不等式对任意及 恒成立？若存在，求的取值范围；若不存在，请说明理由.

．定义域为R的函数满足，且当时，，则当时，的最小值为（   ）

A．

B．

C．

D．

已知函数满足.
（1）求的解析式；
（2）对于（1）中得到的函数，试判断是否存在，使在区间上的值域为？若存在，求出；若不存在，请说明理由.

（1）已知，求的最小值；
（2）已知，求的最大值．

已知二次函数满足，且。
（1）求的解析式；
（2）当时，方程有解，求实数的取值范围；
（3）设，,求的最大值.

已知二次函数（为常数，）的一个零点是．函数，设函数．
（Ⅰ）求的值，当时，求函数的单调增区间；
（Ⅱ）当时，求函数在区间上的最小值；
（Ⅲ）记函数图象为曲线C，设点是曲线C上不同的两点，点M为线段AB的中点，过点M作轴的垂线交曲线C于点N．判断曲线C在点N处的切线是否平行于直线AB？并说明理由．

对于任意a∈[-1,1],函数f(x)=x²+(a-4)x+4-2a的值恒大于零,那么x的取值范围是(　　)

A．(1,3)	B．(-∞,1)∪(3,+∞)
C．(1,2)	D．(3,+∞)

椭圆c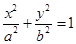：（a>b>0）的离心率为，过其右焦点F与长轴垂直的弦长为1，
（1）求椭圆C的方程；
（2）设椭圆C的左右顶点分别为A，B，点P是直线x=1上的动点，直线PA与椭圆的另一个交点为M，直线PB与椭圆的另一个交点为N，求证：直线MN经过一定点.

已知函数f(x)＝
(1)若x<a时，f(x)<1恒成立，求a的取值范围；
(2)若a≥－4时，函数f(x)在实数集R上有最小值，求实数a的取值范围．

设二次函数满足条件：①；②函数的图像与直线相切．
（1）求函数的解析式；
（2）若不等式在时恒成立，求实数的取值范围．

已知函数和．其中．
（1）若函数与的图像的一个公共点恰好在轴上，求的值；
（2）若和是方程的两根，且满足，证明：当时，．

已知直线y＝mx与函数的图象恰好有3个不同的公共点，则实数m的取值范围是（   ）

A．(，4)

B．(，＋∞)

C．(，5)

D．(，)

已知函数f(x)=x²-2x+3在闭区间［0,m］上最大值为3，最小值为2，则m的取值范围为           

已知函数，其中．
（1）若，且的最大值为，最小值为，试求函数的最小值；
（2）若对任意实数，不等式恒成立，且存在使得成立，求的值；
（3）对于问（1）中的，若对任意的，恒有，求的取值范围．

（本小题满分10分）已知函数f（x）＝x²＋ax＋b的图象关于直线x＝1对称．
（1）求实数a的值
（2）若f（x）的图象过（2，0）点，求x∈[0，3]时f（x）的值域．