设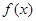 是定义在正整数集上的函数且满足当
是定义在正整数集上的函数且满足当 成立时,总可以推出
成立时,总可以推出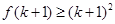 成立,则下列命题总成立的是( )
成立,则下列命题总成立的是( )
A.若 成立 成立 |
B.若 成立,则 成立,则 成立 成立 |
C.若 成立,则当 成立,则当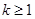 时,均有 时,均有 成立 成立 |
D.若 成立,则当 成立,则当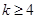 时,均有 时,均有 成立 成立 |
用数学归纳法证明 时,假设n=k时命题成立,则当n=k+1时,左端增加的项数是 ( )
时,假设n=k时命题成立,则当n=k+1时,左端增加的项数是 ( )
| A.1项 | B. 项 项 |
C. 项 项 |
D. 项 项 |
(本小题满分14分)
已知函数 为常数,数列
为常数,数列 满足:
满足: ,
, ,
, .
.
(1)当 时,求数列
时,求数列 的通项公式;
的通项公式;
(2)在(1)的条件下,证明对 有:
有: ;
;
(3)若 ,且对
,且对 ,有
,有 ,证明:
,证明: .
.
把正整数排列成如图甲三角形数阵,然后擦去第偶数行中的奇数和第奇数行中的偶数,得到如图乙的三角形数阵,再把图乙中的数按从小到大的顺序排成一列,得到一个数列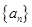 ,若
,若 ,则
,则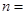 ________.
________.
用数学归纳法证明1+ +
+ +…+
+…+ <n(n∈N*,n>1)时,在证明过程的第二步从n=k到n=k+1时,左边增加的项数是 ( )
<n(n∈N*,n>1)时,在证明过程的第二步从n=k到n=k+1时,左边增加的项数是 ( )
| A.2k | B.2k-1 | C. |
D.2k+1 |
设函数 对任意实数x 、y都有
对任意实数x 、y都有 ,
,
(1)求 的值;
的值;
(2)若 ,求
,求 、
、 、
、 的值;
的值;
(3)在(2)的条件下,猜想
 的表达式,并用数学归纳法加以证明。
的表达式,并用数学归纳法加以证明。
用数学归纳法证明不等式“2n>n2+1对于n≥n0的自然数n都成立”时,第一步证明中的起始值n0应取为________.
在用数学归纳法证明 时,在验证当
时,在验证当 时,等式左边为( )
时,等式左边为( )
| A.1 | B. |
C. |
D. |
试题篮
()