如图,第n个图形是由正n+2边形“扩展”而来,(n=1、2、3、…)则在第n个图形中共有( )个顶点。
| A.(n+1)(n+2) | B.(n+2)(n+3) | C. |
D.n |
如图,△ 是边长为
是边长为 的正三角形,以
的正三角形,以 为圆心,
为圆心, 为半径,沿逆时针方向画圆弧,交
为半径,沿逆时针方向画圆弧,交 延长线于
延长线于 ,记弧
,记弧 的长为
的长为 ;以
;以 为圆心,
为圆心, 为半径,沿逆时针方向画圆弧,交
为半径,沿逆时针方向画圆弧,交 延长线于
延长线于 ,记弧
,记弧 的长为
的长为 ;以
;以 为圆心,
为圆心, 为半径,沿逆时针方向画圆弧,交
为半径,沿逆时针方向画圆弧,交 延长线于
延长线于 ,记弧
,记弧 的长为
的长为 ,则
,则 .如此继续以
.如此继续以 为圆心,
为圆心, 为半径,沿逆时针方向画圆弧,交
为半径,沿逆时针方向画圆弧,交 延长线于
延长线于 ,记弧
,记弧 的长为
的长为 ,
, ,当弧长
,当弧长 时,
时, .
.
如图,在杨辉三角形中,斜线 的上方从1按箭头所示方向可以构成一个“锯齿形”的数列:1,3,3,4,6,5,10, ,记此数列的前
的上方从1按箭头所示方向可以构成一个“锯齿形”的数列:1,3,3,4,6,5,10, ,记此数列的前 项之和为
项之和为 ,则
,则 的值为( )
的值为( )
| A.66 | B.153 | C.295 | D.361 |
把正整数按照下面的表格进行排列
| 1 |
3 |
6 |
10 |
15 |
21 |
…… |
| 2 |
5 |
9 |
14 |
20 |
…… |
…… |
| 4 |
8 |
13 |
19 |
…… |
…… |
…… |
| 7 |
12 |
18 |
…… |
…… |
…… |
…… |
| 11 |
17 |
…… |
…… |
…… |
…… |
…… |
| 16 |
…… |
…… |
…… |
…… |
…… |
…… |
| …… |
…… |
…… |
…… |
…… |
…… |
…… |
则排在第6行,第4列的数是_______________;
排在第 行,第
行,第 列(
列( )的数是______________
)的数是______________
已知大于1的任意一个自然数的三次幂都可表示成连续奇数的和.如:
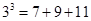

若 是自然数,把
是自然数,把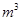 按上述表示,等式右侧的奇数中含有2015,则
按上述表示,等式右侧的奇数中含有2015,则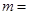 .
.
已知 为正偶数,用数学归纳法证明
为正偶数,用数学归纳法证明

 时,若已假设
时,若已假设 为偶数
为偶数 时命题为真,则还需要用归纳假设再证( )
时命题为真,则还需要用归纳假设再证( )
A. 时等式成立 时等式成立 |
B. 时等式成立 时等式成立 |
C. 时等式成立 时等式成立 |
D. 时等式成立 时等式成立 |
已知整数按如下规律排成一列: 、
、 、
、 、
、 、
、 ,
, ,
, ,
, ,
, ,
, ,……,则第70个数对是( )
,……,则第70个数对是( )
A. |
B. |
C. |
D. |
试题篮
()