用数学归纳法证明某命题时,左式为
 在验证
在验证 时,左边所得的代数式为( )
时,左边所得的代数式为( )
A. |
B. |
C. |
D. |
已知数列 是正数组成的数列,其前n项和
是正数组成的数列,其前n项和 为
为 ,对于一切
,对于一切 均有
均有 与2的等差中项等于
与2的等差中项等于 与2的等比中项。
与2的等比中项。
(1)计算 并由此猜想
并由此猜想 的通项公式
的通项公式 ;
;
(2)用数学归纳法证明(1)中你的猜想。
如图,在杨辉三角形中,斜线 的上方从1按箭头所示方向可以构成一个“锯齿形”的数列:1,3,3,4,6,5,10, ,记此数列的前
的上方从1按箭头所示方向可以构成一个“锯齿形”的数列:1,3,3,4,6,5,10, ,记此数列的前 项之和为
项之和为 ,则
,则 的值为( )
的值为( )
| A.66 | B.153 | C.295 | D.361 |
已知数列{an}的前n项和Sn,a1=﹣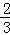 ,Sn+
,Sn+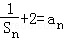 (n≥2).
(n≥2).
(1)计算S1,S2,S3,猜想Sn的表达式并用数学归纳法证明;
(2)设bn=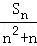 ,数列的{bn}的前n项和为Tn,求证:Tn>﹣
,数列的{bn}的前n项和为Tn,求证:Tn>﹣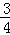 .
.
利用数学归纳法证明不等式 <f(n)(n≥2,n∈N*)的过程中,由n=k变到n=k+1时,左边增加了( )
<f(n)(n≥2,n∈N*)的过程中,由n=k变到n=k+1时,左边增加了( )
| A.1项 | B.k项 | C.2k-1项 | D.2k项 |
给出以下数对序列:
(1,1)
(1,2) (2,1)
(1,3) (2,2) (3,1)
(1,4) (2,3) (3,2) (4,1)
记第 行的第
行的第 个数对为
个数对为 ,如
,如 ,则
,则
(Ⅰ) ________;(Ⅱ)
________;(Ⅱ) ________.
________.
试题篮
()