设函数f(x)=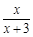 (x>0),观察:f1(x)=f(x)=
(x>0),观察:f1(x)=f(x)=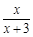 , f2(x)=f(f1(x))=
, f2(x)=f(f1(x))=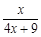 , f3(x)=f(f2(x))=
, f3(x)=f(f2(x))=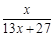 , f4(x)=f(f3(x))=
, f4(x)=f(f3(x))=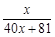 ……根据以上事实,由归纳推理可得:当n∈N*, n≥2时,fn(x)=f(n-1(x))= .
……根据以上事实,由归纳推理可得:当n∈N*, n≥2时,fn(x)=f(n-1(x))= .
某个命题与正整数n有关,如果当 时命题成立,那么可推得当
时命题成立,那么可推得当 时命题也成立. 现已知当
时命题也成立. 现已知当 时该命题不成立,那么可推得( )
时该命题不成立,那么可推得( )
| A.当n=6时该命题不成立 | B.当n=6时该命题成立 |
| C.当n=8时该命题不成立 | D.当n=8时该命题成立 |
已知 为正偶数,用数学归纳法证明
为正偶数,用数学归纳法证明

 时,若已假设
时,若已假设 为偶数
为偶数 时命题为真,则还需要用归纳假设再证( )
时命题为真,则还需要用归纳假设再证( )
A. 时等式成立 时等式成立 |
B. 时等式成立 时等式成立 |
C. 时等式成立 时等式成立 |
D. 时等式成立 时等式成立 |
用火柴棒摆“金鱼”,如图所示:
按照上面的规律,第4个“金鱼”图需要火柴棒的根数为
| A.24 | B.26 | C.28 | D.30 |
某个命题与正整数有关,若当 时该命题成立,那么可推得当
时该命题成立,那么可推得当
 时该命题也成立,现已知当
时该命题也成立,现已知当 时该命题不成立,那么可推得
时该命题不成立,那么可推得
A.当 时,该命题不成立 时,该命题不成立 |
B.当 时,该命题成立 时,该命题成立 |
C.当 时,该命题成立 时,该命题成立 |
D.当 时,该命题不成立 时,该命题不成立 |
把1,3,6,10,15,21这些数叫做三角形数,这是因为这些数目的点子可以排成一个正三角形,则第七个三角形数是 .
已知数列{an}的前n项和Sn,a1=﹣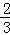 ,Sn+
,Sn+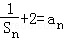 (n≥2).
(n≥2).
(1)计算S1,S2,S3,猜想Sn的表达式并用数学归纳法证明;
(2)设bn=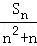 ,数列的{bn}的前n项和为Tn,求证:Tn>﹣
,数列的{bn}的前n项和为Tn,求证:Tn>﹣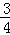 .
.
利用数学归纳法证明不等式 <f(n)(n≥2,n∈N*)的过程中,由n=k变到n=k+1时,左边增加了( )
<f(n)(n≥2,n∈N*)的过程中,由n=k变到n=k+1时,左边增加了( )
| A.1项 | B.k项 | C.2k-1项 | D.2k项 |
给出以下数对序列:
(1,1)
(1,2) (2,1)
(1,3) (2,2) (3,1)
(1,4) (2,3) (3,2) (4,1)
记第 行的第
行的第 个数对为
个数对为 ,如
,如 ,则
,则
(Ⅰ) ________;(Ⅱ)
________;(Ⅱ) ________.
________.
试题篮
()