已知f(n)=(2n+7)·3n+9,存在自然数m,使得对任意n∈N,都能使m整除f(n),则最大的m的值为( )
| A.30 | B.26 | C.36 | D.6 |
设函数f(x)= (x>0),观察:f1(x)=f(x)=
(x>0),观察:f1(x)=f(x)= , f2(x)=f(f1(x))=
, f2(x)=f(f1(x))= , f3(x)=f(f2(x))=
, f3(x)=f(f2(x))= , f4(x)=f(f3(x))=
, f4(x)=f(f3(x))= ……根据以上事实,由归纳推理可得:当n∈N*, n≥2时,fn(x)=f(n-1(x))= .
……根据以上事实,由归纳推理可得:当n∈N*, n≥2时,fn(x)=f(n-1(x))= .
已知数列{an}的前n项和Sn,a1=﹣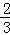 ,Sn+
,Sn+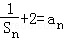 (n≥2).
(n≥2).
(1)计算S1,S2,S3,猜想Sn的表达式并用数学归纳法证明;
(2)设bn=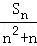 ,数列的{bn}的前n项和为Tn,求证:Tn>﹣
,数列的{bn}的前n项和为Tn,求证:Tn>﹣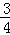 .
.
利用数学归纳法证明不等式 <f(n)(n≥2,n∈N*)的过程中,由n=k变到n=k+1时,左边增加了( )
<f(n)(n≥2,n∈N*)的过程中,由n=k变到n=k+1时,左边增加了( )
| A.1项 | B.k项 | C.2k-1项 | D.2k项 |
给出以下数对序列:
(1,1)
(1,2) (2,1)
(1,3) (2,2) (3,1)
(1,4) (2,3) (3,2) (4,1)
记第 行的第
行的第 个数对为
个数对为 ,如
,如 ,则
,则
(Ⅰ) ________;(Ⅱ)
________;(Ⅱ) ________.
________.
试题篮
()