用数学归纳法证明不等式1+ +
+ +…+
+…+ >
> (n∈N*)成立,其初始值至少应取( )
(n∈N*)成立,其初始值至少应取( )
| A.7 | B.8 | C.9 | D.10 |
在用数学归纳法证明凸n边形内角和定理时,第一步应验证( )
| A.n=1时成立 | B.n=2时成立 |
| C.n=3时成立 | D.n=4时成立 |
是否存在常数a、b、c使等式12+22+32+…+n2+(n-1)2+…+22+12=an(bn2+c)对于一切n∈N*都成立,若存在,求出a、b、c并证明;若不存在,试说明理由.
如图所示,∠AOB=1rad,点Al,A2, 在OA上,点B1,B2, 在OB上,其中的每一个实线段和虚线段的长均为1个长度单位,一个动点M从O点出发,沿着实线段和以O为圆心的圆弧匀速运动,速度为l长度单位/秒,则质点M到达A3点处所需要的时间为 秒,质点M到达An点处所需要的时间为 秒.

已知数列{an}的前n项和Sn,a1=﹣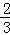 ,Sn+
,Sn+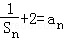 (n≥2).
(n≥2).
(1)计算S1,S2,S3,猜想Sn的表达式并用数学归纳法证明;
(2)设bn=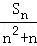 ,数列的{bn}的前n项和为Tn,求证:Tn>﹣
,数列的{bn}的前n项和为Tn,求证:Tn>﹣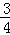 .
.
利用数学归纳法证明不等式 <f(n)(n≥2,n∈N*)的过程中,由n=k变到n=k+1时,左边增加了( )
<f(n)(n≥2,n∈N*)的过程中,由n=k变到n=k+1时,左边增加了( )
| A.1项 | B.k项 | C.2k-1项 | D.2k项 |
给出以下数对序列:
(1,1)
(1,2) (2,1)
(1,3) (2,2) (3,1)
(1,4) (2,3) (3,2) (4,1)
记第 行的第
行的第 个数对为
个数对为 ,如
,如 ,则
,则
(Ⅰ) ________;(Ⅱ)
________;(Ⅱ) ________.
________.
试题篮
()