已知向量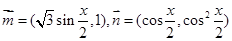 .记
.记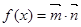
(I)求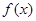 的最小正周期及单调增区间;
的最小正周期及单调增区间;
(Ⅱ)在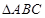 中,角
中,角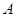 ,
,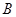 ,
,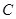 的对边分别为
的对边分别为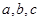 若
若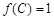 ,
,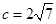 ,
,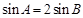 ,求
,求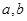 的值.
的值.
已知角A、B、C为△ABC的三个内角,其对边分别为a、b、c,若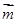 =(-cos
=(-cos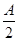 ,sin
,sin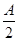 ),
),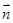 =(cos
=(cos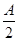 ,sin
,sin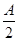 ),a=2
),a=2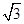 ,且
,且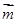 ·
·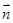 =
=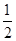 .
.
(1)若△ABC的面积S=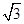 ,求b+c的值.
,求b+c的值.
(2)求b+c的取值范围.
在 中,角A、B、C的对边分别为
中,角A、B、C的对边分别为 、
、 、
、 ,已知向量
,已知向量 、
、 ,且
,且 .
.
(1)求角 的大小;
的大小;
(2)若 ,求
,求 面积的最大值.
面积的最大值.
如图,塔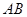 底部为点
底部为点 ,若
,若 两点相距为100m并且与点
两点相距为100m并且与点 在同一水平线上,现从
在同一水平线上,现从 两点测得塔顶
两点测得塔顶 的仰角分别为
的仰角分别为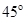 和
和 ,则塔
,则塔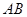 的高约为(精确到0.1m,
的高约为(精确到0.1m, ,
, )( )
)( )

| A.36.5 | B.115.6 | C.120.5 | D.136.5 |
已知△ABC的一个内角为120°,并且三边长构成公差为4的等差数列,则△ABC的面积为 .
在△ABC中,a,b,c分别为∠A,∠B,∠C的对边,且c>b>a,若向量 =(a-b,1)和
=(a-b,1)和 =(b-c,1)平行,且sin B=
=(b-c,1)平行,且sin B= ,当△ABC的面积为
,当△ABC的面积为 时,则b=( )
时,则b=( )
A. |
B.2 | C.4 | D.2+ |
试题篮
()