如图,一货轮航行到M处,测得灯塔S在货轮的北偏东15°,与货轮相距20海里,随后货轮按北偏西30°的方向航行,30分钟后又测得灯塔在货轮的东北方向,则货轮航行的速度为( )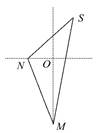
A.20(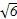 + + )海里/小时 )海里/小时 |
B.20(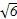 - - )海里/小时 )海里/小时 |
C.20(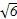 + + )海里/小时 )海里/小时 |
D.20(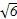 - - )海里/小时 )海里/小时 |
(本小题满分12分)如图,为测得河对岸某建筑物AB的高,先在河岸上选一点C,使C在建筑物底端B的正东方向上,测得点A的仰角为60°,再由点C沿东偏北75°方向走20米到达位置D,测得∠BDC=30°。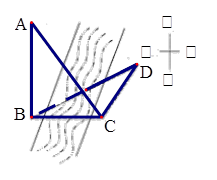
(Ⅰ)求sⅠn∠BCD的值;
(Ⅱ)求此建筑物的高度.
如图,在等腰直角△OPQ中,∠POQ=90°,OP=2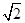 ,点M在线段PQ上.
,点M在线段PQ上.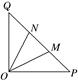
(1)若OM=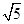 ,求PM的长;
,求PM的长;
(2)若点N在线段MQ上,且∠MON=30°,问:当∠POM取何值时,△OMN的面积最小?并求出面积的最小值.
(本小题满分12分)设 的内角
的内角 所对应的边长分别是
所对应的边长分别是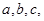 且
且
(Ⅰ)当 时,求
时,求 的值;
的值;
(Ⅱ)当 的面积为3时,求
的面积为3时,求 的值.
的值.
已知△ABC的一个内角为120°,并且三边长构成公差为4的等差数列,则△ABC的面积为 .
在△ABC中,a,b,c分别为∠A,∠B,∠C的对边,且c>b>a,若向量 =(a-b,1)和
=(a-b,1)和 =(b-c,1)平行,且sin B=
=(b-c,1)平行,且sin B= ,当△ABC的面积为
,当△ABC的面积为 时,则b=( )
时,则b=( )
A. |
B.2 | C.4 | D.2+ |
在△ 中,角
中,角 、
、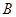 、
、 所对的边分别为
所对的边分别为 、
、 、
、 ,已知
,已知 (
( ),且
),且 .
.
(1)当 ,
, 时,求
时,求 ,
, 的值;
的值;
(2)若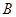 为锐角,求实数
为锐角,求实数 的取值范围.
的取值范围.
试题篮
()