已知函数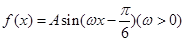 相邻两个对称轴之间的距离是
相邻两个对称轴之间的距离是 ,且满足,
,且满足,
(1)求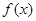 的单调递减区间;
的单调递减区间;
(2)在钝角△ABC中,a、b、c分别为角A、B、C的对边,sinB=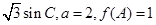 ,求△ABC的面积。
,求△ABC的面积。
辽宁广播电视塔位于沈阳市沈河区青年公园西侧,蜿蜒的南运河带状公园内,占地8000平方米.全塔分为塔座、塔身、塔楼和桅杆四部分.某数学活动小组在青年公园内的A处测得塔顶B处的仰角为45°. 在水平地面上,沿着A点与塔底中心C处连成的直线行走129米后到达D处(假设可以到达),此时测得塔顶B处的仰角为60°.
(1)请你根据题意,画出一个ABCD四点间的简单关系图形;
(2)根据测量结果,计算辽宁广播电视塔的高度(精确到1米).
(本小题满分12分)如图,山脚下有一小塔AB,在塔底B测得山顶C的仰角为60°,在山顶C测得塔顶A的俯角为45°,已知塔高AB=20 m,求山高CD.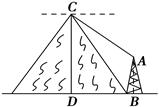
已知向量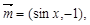 ,
,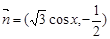 ,函数
,函数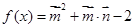 .
.
(1)求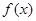 的最大值,并求取最大值时
的最大值,并求取最大值时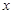 的取值集合;
的取值集合;
(2)已知 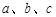 分别为
分别为 内角
内角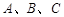 的对边,且
的对边,且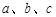 成等比数列,角
成等比数列,角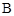 为锐角,且
为锐角,且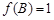 ,求
,求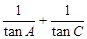 的值.
的值.
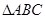 中,角
中,角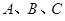 所对的边分别为
所对的边分别为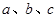 ,下列命题正确的是________(写出正确命题的编号).
,下列命题正确的是________(写出正确命题的编号).
①若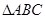 最小内角为
最小内角为 ,则
,则 ;
;
②若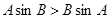 ,则
,则 ;
;
③存在某钝角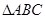 ,有
,有 ;
;
④若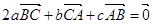 ,则
,则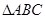 的最小角小于
的最小角小于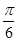 ;
;
⑤若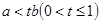 ,则
,则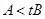 .
.
已知向量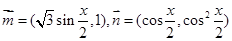 .记
.记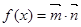
(I)求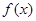 的最小正周期及单调增区间;
的最小正周期及单调增区间;
(Ⅱ)在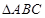 中,角
中,角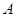 ,
,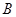 ,
,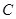 的对边分别为
的对边分别为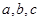 若
若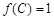 ,
,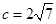 ,
,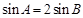 ,求
,求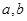 的值.
的值.
已知△ABC的一个内角为120°,并且三边长构成公差为4的等差数列,则△ABC的面积为 .
在△ABC中,a,b,c分别为∠A,∠B,∠C的对边,且c>b>a,若向量 =(a-b,1)和
=(a-b,1)和 =(b-c,1)平行,且sin B=
=(b-c,1)平行,且sin B= ,当△ABC的面积为
,当△ABC的面积为 时,则b=( )
时,则b=( )
A. |
B.2 | C.4 | D.2+ |
在△ 中,角
中,角 、
、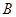 、
、 所对的边分别为
所对的边分别为 、
、 、
、 ,已知
,已知 (
( ),且
),且 .
.
(1)当 ,
, 时,求
时,求 ,
, 的值;
的值;
(2)若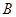 为锐角,求实数
为锐角,求实数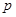 的取值范围.
的取值范围.
试题篮
()