(本小题满分14分)在△ABC中,角A、B、C的对边分别为a、b、c.
(1) 若sin =2cos A,求A的值;
=2cos A,求A的值;
(2) 若cosA= ,b=3c,求sinC的值.
,b=3c,求sinC的值.
.(本小题满分13分)
已知D为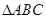 的边BC上一点,且
的边BC上一点,且
(1)求角A的大小;
(2)若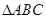 的面积为
的面积为 ,且
,且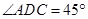 ,求BD的长。
,求BD的长。
(本小题满分12分)某城市有一块不规则的绿地如图所示,城建部门欲在该地上建造一个底座为三角形的环境标志,小李、小王设计的底座形状分别为△ABC、△ABD,经测量AD=BD=14,BC=10,AC=16,∠C=∠D.
(I)求AB的长度;
(Ⅱ)若建造环境标志的费用与用地面积成正比,不考虑其他因素,小李、小王谁的设计使建造费用最低,请说明理由.
.(本小题满分12分)
设 的内角
的内角 的对边分别为
的对边分别为 ,且
,且 ,求:
,求:
(1)角 的值;
的值;
(2)函数 在区间
在区间 上的最大值及对应的x值.
上的最大值及对应的x值.
(本小题满分12分)一缉私艇发现在北偏东 方向,距离12 nmile的海面上有一走私船正以10 nmile/h的速度沿东偏南
方向,距离12 nmile的海面上有一走私船正以10 nmile/h的速度沿东偏南 方向逃窜.缉私艇的速度为14 nmile/h, 若要在最短的时间内追上该走私船,缉私艇应沿北偏东
方向逃窜.缉私艇的速度为14 nmile/h, 若要在最短的时间内追上该走私船,缉私艇应沿北偏东 的方向去追,.求追及所需的时间和
的方向去追,.求追及所需的时间和 角的正弦值.
角的正弦值.
(本小题满分12分)
如下图,互相垂直的两条公路 、
、 旁有一矩形花园
旁有一矩形花园 ,现欲将其扩建成一个更大的三角形花园
,现欲将其扩建成一个更大的三角形花园 ,要求点
,要求点 在射线
在射线 上,点
上,点 在射线
在射线 上,且直线
上,且直线 过点
过点 ,其中
,其中 米,
米, 米. 记三角形花园
米. 记三角形花园 的面积为
的面积为 .
.
(Ⅰ)问: 取何值时,
取何值时, 取得最小值,并求出最小值;
取得最小值,并求出最小值;
(Ⅱ)若 不超过1764平方米,求
不超过1764平方米,求 长的取值范围.
长的取值范围.
试题篮
()