高中数学西姆松定理解答题

（本小题满分12分）
在中，角、、的对边分别为、、，且满足.
（1）求角的大小；
（2）当时，求的面积.

(本题满分14分）
在中，角A、B、C所对的边分别为a，b，c，，且
（1）求的值；
（2）若，求bc的最大值.

（本小题满分12分）在中，，，是角，，的对边，若,且，（1）求的面积；（2）若，求和的值．

(12分)在△ABC中，角A、B、C所对的边分别为a、b、c，且b²＋c²＝a²＋bc．
(1)求角A的大小；
(2)若sin B·sin C＝sin²A，试判断△ABC的形状．

在△ABC中，已知，，B=45°， 求A、C及c

（（本小题满分12分）
炮兵阵地位于地面处，两观察所分别位于地面点和处，已知，  ，, 目标出现于地面点处时，测得， (如答题卷图所示）.求：炮兵阵地到目标的距离.

已知中，.
（1）求的面积;
（2）求的值.

港口北偏东方向的处有一检查站，港口正东方向的处有一轮船，距离检查站为31海里，该轮船从处沿正西方向航行20海里后到达处观测站，已知观测站与检查站距离21海里，问此时轮船离港口还有多远？

C

              

B

A

D

    

(10分) 如图所示，已知、两点的距离为海里，在的北偏东处，甲船自以海里/小时的速度向航行，同时乙船自以海里/小时的速度沿方位角方向航行。问航行几小时两船之间的距离最短？

在中，角的对边分别为，且．
（1）求角的大小；
（2）若，求的面积．

如图，△ACD是等边三角形，△ABC是等腰直角
三角形，∠ACB=90°，BD交AC于E，AB=2.
（1）求cos∠CBE的值；（2）求AE。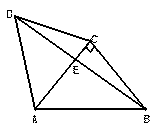

如图，当甲船位于A处时获悉，在其正东方向相距20海里的B处有一艘渔船遇险等待营救．甲船立即前往救援，同时把消息告知在甲船的南偏西30，相距10海里C处的乙船，试问乙船应朝北偏东多少度的方向沿直线前往B处救援？（可能用到的数据，）

（本小题满分12分）
在中，内角对边的边长分别是，已知，。
（Ⅰ）若的面积等于，求。
（Ⅱ）若，求的面积。