设原命题:若a+b≥2,则a,b 中至少有一个不小于1。则原命题与其逆命题
的真假情况是( )
| A.原命题真,逆命题假 | B.原命题假,逆命题真 |
| C.原命题与逆命题均为真命题 | D.原命题与逆命题均为假命题 |
以下命题中:①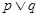 为假命题,则
为假命题,则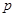 与
与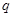 均为假命题
均为假命题
②对具有线性相关的变量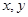 有一组观测数据
有一组观测数据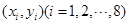 ,其回归直线方程是
,其回归直线方程是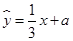 ,且
,且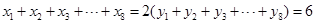 ,则实数
,则实数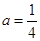
③对于分类变量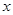 与
与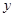 它们的随机变量
它们的随机变量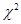 的观测值
的观测值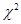 来说
来说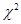 越小.“
越小.“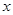 与
与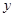 有关联”的把握程度越大
有关联”的把握程度越大
④已知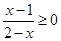 ,则函数
,则函数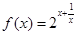 的最小值为16. 其中真命题的个数为 ( )
的最小值为16. 其中真命题的个数为 ( )
| A.0 | B.1 | C.2 | D.3 |
下列命题中的真命题是( )
A.对于实数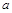 、b、c,若 、b、c,若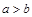 ,则 ,则 |
| B.x2>1是x>1的充分而不必要条件 |
C. ,使得 ,使得 成立 成立 |
D. , ,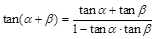 成立 成立 |
已知命题 :函数
:函数 的最小正周期为
的最小正周期为 ;命题
;命题 :若函数
:若函数 为偶函数,则
为偶函数,则 关于
关于 对称.则下列命题是真命题的是( )
对称.则下列命题是真命题的是( )
A. |
B. |
C. |
D. |
给出下列命题,其中真命题的个数是( )
①存在 ,使得
,使得 成立;
成立;
②对于任意的三个平面向量 、
、 、
、 ,总有
,总有 成立;
成立;
③相关系数 (
( ),
), 值越大,变量之间的线性相关程度越高.
值越大,变量之间的线性相关程度越高.
| A.0 | B.1 | C.2 | D.3 |
下列说法正确的是( )
A.命题“若 ,则 ,则 ”的否命题为:“若 ”的否命题为:“若 ,则 ,则 ” ” |
B.若命题 ,则命题 ,则命题 |
C.命题“若 ,则 ,则 ”的逆否命题为真命题 ”的逆否命题为真命题 |
D.“ ”是“ ”是“ ”的必要不充分条件 ”的必要不充分条件 |
设命题p:方程x2+3x-1=0的两根符号不同;命题q:方程x2+3x-1=0的两根之和为3,判断命题“Øp”、“Øq”、“p∧q”、“p∨q”为假命题的个数为( )
| A.0 | B.1 | C.2 | D.3 |
下列命题中是假命题的是( )
| A.∃α,β∈R,使sin(α+β)=sinα+sinβ |
B.∀ ∈R,函数f(x)=sin(2x+ ∈R,函数f(x)=sin(2x+ )都不是偶函数 )都不是偶函数 |
C.∃m∈R,使f(x)=(m-1)· 是幂函数,且在(0,+∞)上单调递减 是幂函数,且在(0,+∞)上单调递减 |
| D.∀a>0,函数f(x)=ln2x+lnx-a有零点 |
对于命题p:∀x∈[0,+∞),(log32)x≤1,( )
A.是假命题, p:∃x0∈[0,+∞), p:∃x0∈[0,+∞), >1 >1 |
B.是假命题, p:∀x∈[0,+∞),(log32)x≥1 p:∀x∈[0,+∞),(log32)x≥1 |
C.是真命题, p:∃x0∈[0,+∞), p:∃x0∈[0,+∞),  >1 >1 |
D.是真命题, p:∀x∈[0,+∞),(log32)x≥1 p:∀x∈[0,+∞),(log32)x≥1 |
对于非空实数集A,记A*={y|∀x∈A,y≥x}.设非空实数集合M、P满足:M⊆P,且若x>1,则x∉P.现给出以下命题:
①对于任意给定符合题设条件的集合M、P,必有P*⊆M*;
②对于任意给定符合题设条件的集合M、P,必有M*∩P≠∅;
③对于任意给定符合题设条件的集合M、P,必有M∩P*=∅;
④对于任意给定符合题设条件的集合M、P,必存在常数a,使得对任意的b∈M*,恒有a+b∈P*.其中正确的命题是( )
| A.①③ | B.③④ |
| C.①④ | D.②③ |
下列说法中,不正确的是( )
A.命题p:∀x∈R,sinx≤1,则 p:∃x∈R,sinx>1 p:∃x∈R,sinx>1 |
B.在△ABC中,“A>30°”是“sinA> ”的必要不充分条件 ”的必要不充分条件 |
C.命题p:点( ,0)为函数f(x)=tan(2x+ ,0)为函数f(x)=tan(2x+ )的一个对称中心;命题q:如果|a|=1,|b|=2,<a,b>=120°,那么b在a方向上的投影为1,则( )的一个对称中心;命题q:如果|a|=1,|b|=2,<a,b>=120°,那么b在a方向上的投影为1,则( p)∨( p)∨( q)为真命题 q)为真命题 |
| D.命题“在△ABC中,若sinA=sinB,则△ABC为等腰三角形”的否命题为真命题 |
有关命题的说法错误的是( )
| A.命题“若x2-3x+2=0,则x=1”的逆否命题为:“若x≠1,则x2-3x+2≠0” |
| B.“x=1”是“x2-3x+2=0”的充分而不必要条件 |
| C.若p∧q为假命题,则p,q均为假命题 |
D.对于命题p:∃x∈R,使得x2+x+1<0.则 p:∀x∈R,均有x2+x+1≥0 p:∀x∈R,均有x2+x+1≥0 |
已知a,b,c都是实数,则在命题“若a>b,则ac2>bc2”与它的逆命题、否命题、逆否命题这四个命题中,真命题的个数是( )
| A.4 | B.2 | C.1 | D.0 |
下列命题中正确命题的个数是( )
(1)命题“若 ,则
,则 ”的逆否命题为“若
”的逆否命题为“若 ,则
,则 ”;
”;
(2)设回归直线方程 中,
中, 增加1个单位时,
增加1个单位时, 一定增加2个单位;
一定增加2个单位;
(3)若 为假命题,则
为假命题,则 均为假命题;
均为假命题;
(4)对命题 ,使得
,使得 ,则
,则 ,均有
,均有 ;
;
| A.1 | B.2 | C.3 | D.4 |
试题篮
()