高中数学表面展开图选择题

在棱长为2的正方体ABCD－A₁B₁C₁D₁中，点O为底面ABCD的中心，在正方体ABCD－A₁B₁C₁D₁内随机取一点P，则点P到点O的距离大于1的概率为（注：球的体积公式）

A．

B．1－

C．

D．1－

若平行于圆锥底面的平面将圆锥的高平分，则圆锥被分成的两部分的侧面积比是 （    ）

A．1:1

B．1:2

C．1:3

D．1:4

将棱长为2的正方体木块切削成一个体积最大的球，则该球的体积为      （ ▲ ）

A．

B．

C．

D．

六棱柱的底面是边长为3的正六边形,侧面是矩形,侧棱长为4,则其侧面积等于

A．12

B．48

C．64

D．72

五棱台ABCDE-A₁B₁C₁D₁E₁的表面积是30,侧面积等于25,则两底面积的和等于

A．5

B．25

C．30

D．55

一个与球心距离为1的平面截球体所得的圆面面积为，则球的体积为(  )

A． 8

B．

C．

D．

圆x2＋(y＋1)2＝3绕直线kx－y－1＝0旋转一周所得的几何体的体积为   (　　)

A．36π

B．12π

C．4π

D．4π

正方体的表面积是a²，它的顶点都在一个球面上，则这个球的表面积是
(　　)

A．	B．
C．2πa^2	D．3πa^2

底面半径为2，高为4的圆柱，它的侧面积是（　　）

A．8p

B．16p

C．20p

D．24p

在平面上，若两个正三角形的边长比为1:2.则它们的面积之比为1:4.类似地，在空间中，若两个正四面体的棱长比为1:2，则它们的体积比为（ ）

A．1:2

B．1:4

C．1:6

D．1:8

做一个容积为的圆柱形封闭容器，要使所用的材料最省，底面直径为    （   ）

A．

B．

C．

D．

正六棱锥的斜高为cm，侧面与底面所成的角为30°，则它的体积为 （ ）

A．

B．

C．

D．

（（本小题满分12分）
如图，多面体ABCD—EFG中，底面ABCD为正方形，GD//FC//AE，AE⊥平面ABCD，其正视图、俯视图如下：

（I）求证：平面AEF⊥平面BDG；
（II）若存在使得，二面角A—BG—K的大小为，求的值。

在正三棱柱中，若，，则点到平面的距离为（ ）

A.                B.                C.             D.

半径为2的球面上冇P,M,N,R四点，且PM,PN,PR两两垂直，则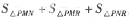的最大值为

A．8

B．12

C．16

D．24