高中数学表面展开图选择题

如图，已知点P在圆柱OO₁的底面⊙O上，AB、A₁B₁分别为⊙O、⊙O₁的直径，且A₁A⊥平面PAB.
(1)求证：BP⊥A₁P；
(2)若圆柱OO₁的体积V＝12π，OA＝2，∠AOP＝120°，求三棱锥A₁－APB的体积．
(3)在AP上是否存在一点M，使异面直线OM与A₁B所成角的余弦值为 ？若存在，请指出M的位置，并证明；若不存在，请说明理由.

一个正方体的顶点都在球面上，它的棱长为4ｃｍ，则球的表面积是

A．32Лｃｍ^２

B．48Лｃｍ^２

C．64Лｃｍ^２

D．80Лｃｍ^２

：在四面体ABCD中，设AB＝1，CD＝，直线AB与CD的距离为2，夹角为，则四面体ABCD的体积等于
A．             B．        C．               D．       

已知四面体的棱长均为2，其正视图是边长为2的等边三角形（如图，其  
中为水平线），则其侧视图的面积是

A．

B．

C．

D．

正方体的内切球与其外接球的体积之比为          （   ）             
A　1∶          B　1∶3            　C　1∶3         　D　1∶9

长方体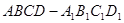的长，宽，高分别是3，2,1，则该长方体的体对角线是（  ）

A．

B．

C．

D．

已知正方体外接球的体积是，那么正方体的棱长等于 （   ）

A．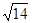

B．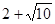

C．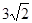

D．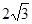

设长方体的长、宽、高分别为2a、a、a，其顶点都在一个球面上，则该球的表面积为（    ）

A．

B．

C．

D．

一个四棱锥和一个三棱锥恰好可以拼接成一个三棱柱，这个四棱锥的底面为正方形，且底面边长与各侧棱长相等，这个三棱锥的底面边长与各侧棱长也都相等．设四棱锥、三棱锥、三棱柱的高分别为，，，则（  　）

A．

B．

C．

D．

正三棱锥的底面边长为2，侧面均为直角三角形，则此棱锥的体积为（  ）

A．

B．

C．

D．

若圆柱、圆锥的底面直径和高都等于球的直径，则圆柱、圆锥、球的体积的比为（  ）

A．1:2:3

B．2：3：4

C．3:2:4

D．3:1:2

长方体的过一个顶点的三条棱长的比是1：2：3，对角线长为，则这个长方体的体积为（   ）

A．6

B．12

C．24

D．48

已知两个球的表面积之比为，则这两个球的半径之比为（     ）

A．

B．

C．

D．

直三棱柱中，各侧棱和底面的边长均为，点是上任意一点，
连接，则三棱锥的体积为
A          B.          C．            D.

如图所示，一个空间几何体的正视图和侧视图都是边长为1的正方形，俯视图是一个圆，那么这个几何体的侧面积为（    ）

A．

B．

C．

D．