高中数学表面展开图试题

已知某几何体的三视图如图所示，则该几何体的表面积等于（  ）

A．

B．160

C．

D．

如图，已知四边形和都是菱形，平面和平面互相垂直，且．

（Ⅰ）求证：
（Ⅱ）求四面体的体积．

利用一个球体毛坯切削后得到一个四棱锥,其中底面四边形是边长为的正方形，，且平面,则球体毛坯体积的最小值应为       ．

直角梯形，满足,现将其沿折叠成三棱锥，当三棱锥体积取最大值时其外接球的体积为（   ）

A．

B．

C．

D．

平面四边形中，，，，将其沿对角线折成四面体，使平面平面，若四面体的顶点在同一个球面上，则该球的体积为 （   ）

A．

B．

C．

D．

如果圆柱轴截面的周长为定值，则其体积的最大值为（  ）

A．p

B．p

C．p

D．p

长方体的一个顶点上三条棱长为3、4、5，且它的八个顶点都在一个球面上，这个球的表面积是（ ）

A．20π

B．25π

C．50π

D．200π

如图，已知平面ABCD，四边形ABEF为矩形，四边形ABCD为直角梯形，，，，.

（1）求证：平面BCE；
（2）求证：平面BCE；
（3）求三棱锥的体积.

如图，在三棱柱中，侧棱底面ABC，AB⊥BC，D为AC的中点，．

（1）求证：平面；
（2）设BC=3，求四棱锥的体积．

如图是某直三棱柱被削去上底后的直观图与三视图的侧视图、俯视图，在直观图中，M是BD的中点，，侧视图是直角梯形，俯视图是等腰直角三角形，有关数据如图所示．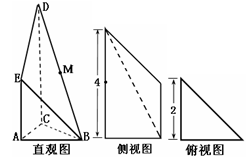

（Ⅰ）求出该几何体的体积；
（Ⅱ）试问在边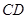上是否存在点N，使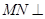平面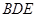？ 若存在，确定点N的位置（不需证明）；若不存在，请说明理由．

如图，在直三棱柱ABC­A₁B₁C₁中，AB＝AC＝5，BB₁＝BC＝6，D，E分别是AA₁和B₁C的中点．

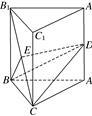
（1）求证：DE∥平面ABC；
（2）求三棱锥E­BCD的体积．

如图，在三棱柱中，侧棱垂直于底面，AB⊥BC，AA₁＝AC＝2，BC＝1，E，F分别是A₁C₁，BC的中点．

（1）求证：平面ABE⊥平面B₁BCC₁；
（2）求证：C₁F∥平面ABE；
（3）求三棱锥E —ABC的体积.

已知矩形ABCD,ED⊥平面ABCD，EF//DC．EF=DE=AD==2，O为BD中点.
（Ⅰ）求证：EO//平面BCF；
（Ⅱ）求几何体ABCDEF的体积.

（本小题满分12分）如图：是直径为的半圆，为圆心,是上一点，
且.，且，，为的中点，为的中点，为上一点,且.

（Ⅰ）求证： 面⊥面；
（Ⅱ）求证：∥平面；
（Ⅲ）求三棱锥的体积.

（本小题满分12分）如图，矩形中，对角线的交点为⊥平面为上的点，且．
（I）求证：⊥平面；
（II）求三棱锥的体积．