(本小题满分14分)已知函数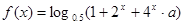 ;
;
(1)若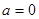 ,求
,求 的值域;(2)在(1)的条件下,判断
的值域;(2)在(1)的条件下,判断 的单调性;(3)当
的单调性;(3)当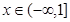 时
时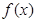 有意义求实
有意义求实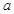 的范围。
的范围。
(本小题满分12分)函数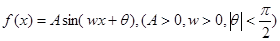 的一系列对应值如下表:
的一系列对应值如下表:
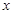 |
。。。 |
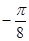 |
0 |
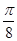 |
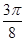 |
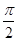 |
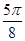 |
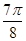 |
。。。 |
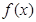 |
。。。 |
0 |
1 |
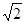 |
0 |
—1 |
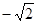 |
0 |
。。。 |
(1)根据表中数据求出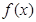 的解析式;
的解析式;
(2)指出函数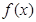 的图象是由函数
的图象是由函数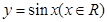 的图象经过怎样的变化而得到的;
的图象经过怎样的变化而得到的;
(3)令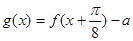 ,若
,若 在
在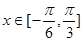 时有两个零点,求
时有两个零点,求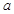 的取值范围。
的取值范围。
(本小题满分12分)在矩形ABCD中,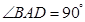
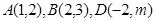 ;(1)求
;(1)求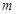 的值和点C的坐标?
的值和点C的坐标?
(2)求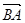 与
与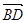 夹角
夹角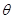 的余弦值;
的余弦值;
(本小题满分12分)
设M是由满足下列条件的函数 构成的集合:“①方程
构成的集合:“①方程 有实数根;②函数
有实数根;②函数 ”
”
(I)判断函数 是否是集合M中的元素,并说明理由;
是否是集合M中的元素,并说明理由;
(II)集合M中的元素 具有下面的性质:若
具有下面的性质:若 的定义域为D,则对于任意
的定义域为D,则对于任意 成立。试用这一性质证明:方程
成立。试用这一性质证明:方程 只有一个实数根;
只有一个实数根;
(III)对于M中的函数 的实数根,求证:对于
的实数根,求证:对于 定义域中任意的
定义域中任意的 当
当 且
且
(本小题满分12分)
已知函数
(I)若 在区间
在区间 上是增函数,求实数a的取值范围;
上是增函数,求实数a的取值范围;
(II)若 的一个极值点,求
的一个极值点,求 上的最大值;
上的最大值;
(III)在(II)的条件下,是否存在实数b,使得函数
 的图象恰有3个交点,若存在,请求出实数b的取值范围;若不存在,试说明理由。
的图象恰有3个交点,若存在,请求出实数b的取值范围;若不存在,试说明理由。
(本小题满分12分)如图,在三棱锥 中,
中, 底面
底面 ,
,
点 ,
, 分别在棱
分别在棱 上,且
上,且
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)当 为
为 的中点时,求
的中点时,求 与平面
与平面 所成的角的余弦值;
所成的角的余弦值;
(Ⅲ)是否存在点 使得二面角
使得二面角 为直二面角?并说明理由.
为直二面角?并说明理由.
(本小题满分12分)在直三棱柱ABC—A1B1C1中,∠ ACB=90°,AC=BC=AA1=1,D、E分别为棱AB、
ACB=90°,AC=BC=AA1=1,D、E分别为棱AB、 BC的中点,M为棱AA1上的点。
BC的中点,M为棱AA1上的点。
(1)证明:A1B1⊥C1D;
(2)当 的大小。
的大小。
试题篮
()