(本小题满分12分)如图1,在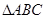 中,
中,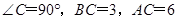 ,
,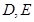 分别是
分别是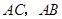 上的点,且
上的点,且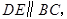
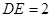 .将
.将 沿
沿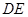 折起到
折起到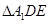 的位置,使
的位置,使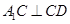 ,如图2.
,如图2.
(Ⅰ)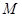 是
是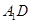 的中点,求
的中点,求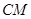 与平面
与平面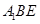 所成角的大小;
所成角的大小;
(Ⅱ)求二面角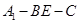 的正切值.
的正切值.
(本小题满分14分)椭圆 ,椭圆的左、右焦点分别为
,椭圆的左、右焦点分别为 ,椭圆上的点到中心的最短距离为
,椭圆上的点到中心的最短距离为 ,且椭圆上的点到左焦点
,且椭圆上的点到左焦点 的最长距离为
的最长距离为 .
.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)若直线 交
交 于A,B两点.若AB的中点坐标的纵坐标为
于A,B两点.若AB的中点坐标的纵坐标为 ,求
,求 的面积.
的面积.
(本小题满分12分)已知数列 是各项均为正数的等差数列,其中
是各项均为正数的等差数列,其中 ,且
,且 成等比数列;数列
成等比数列;数列 的前
的前 项和为
项和为 ,满足
,满足 .
.
(Ⅰ)求数列 ,
, 的通项公式;
的通项公式;
(Ⅱ)如果 ,设数列
,设数列 的前
的前 项和为
项和为 ,是否存在正整数
,是否存在正整数 ,使得
,使得 成立,若存在,求出
成立,若存在,求出 的最小值,若不存在,说明理由.
的最小值,若不存在,说明理由.
(本小题满分13分)如图,在多面体ABCDEF中,底面ABCD是边长为2的菱形,∠BAD=60°,四边形BDEF是矩形,平面BDEF⊥平面ABCD,BF=3,H是CF的中点.
(Ⅰ)求证:AF//平面BDH;
(Ⅱ)求二面角A﹣FE﹣C的大小.
已知椭圆 (a>b>0)的两个焦点分别为
(a>b>0)的两个焦点分别为 ,离心率为
,离心率为 ,过
,过 的直线l与椭圆C交于M,N两点,且
的直线l与椭圆C交于M,N两点,且 的周长为8.
的周长为8.
(Ⅰ)求椭圆C的方程;
(Ⅱ)过原点O的两条互相垂直的射线与椭圆C分别交于A,B两点,证明:点O到直线AB的距离为定值,并求出这个定值.
已知某校 四个社团的学生人数分别为10,5,20,15.现为了了解社团活动开展情况,用分层抽样的方法从
四个社团的学生人数分别为10,5,20,15.现为了了解社团活动开展情况,用分层抽样的方法从 四个社团的学生当中随机抽取10名学生参加问卷调查.
四个社团的学生当中随机抽取10名学生参加问卷调查.
(Ⅰ)从 四个社团中各抽取多少人?
四个社团中各抽取多少人?
(Ⅱ)在社团 所抽取的学生总数中,任取2个,求
所抽取的学生总数中,任取2个,求 社团中各有1名学生的概率.
社团中各有1名学生的概率.
(本小题满分12分)
小王在某社交网络的朋友圈中,向在线的甲、乙、丙随机发放红包,每次发放1个.
(Ⅰ)若小王发放5元的红包2个,求甲恰得1个的概率;
(Ⅱ)若小王发放3个红包,其中5元的2个,10元的1个.记乙所得红包的总钱数为X,求X的分布列和期望.
(本小题满分12分)已知等差数列 ,
, 为其前
为其前 项和,
项和,
(1)求数列 的通项公式;
的通项公式;
(2)若 ,求数列
,求数列 的前
的前 项和
项和
试题篮
()