已知函数f(x)=|x﹣4|﹣t,t∈R,且关于x的不等式f(x+2)≤2的解集为[﹣1,5].
(1)求t值;
(2)a,b,c均为正实数,且a+b+c=t,求证: +
+ +
+ ≥1.
≥1.
某市随机抽取一年(365天)内100天的空气质量指数API的监测数据,结果统计如下:
| API |
[0,50] |
(50,100] |
(100,150] |
(150,200] |
(200,250] |
(250,300] |
>300 |
| 空气质量 |
优 |
良 |
轻微污染 |
轻度污染 |
中度污染 |
中度重污染 |
重度污染 |
| 天数 |
4 |
13 |
18 |
30 |
9 |
11 |
15 |
记某企业每天由于空气污染造成的经济损失为S(单位:元),空气质量指数API为ω,在区间[0,100]对企业没有造成经济损失;在区间(100,300]对企业造成经济损失成直线模型(当API为150时造成的经济损失为500元,当API为200时,造成的经济损失为700元);当API大于300时造成的经济损失为2000元.
(1)试写出S(ω)表达式;
(2)试估计在本年内随机抽取一天,该天经济损失S大于500元且不超过900元的概率;
(3)若本次抽取的样本数据有30天是在供暖季,其中有8天为重度污染,完成下面2×2列联表,并判断能否有95%的把握认为该市本年空气重度污染与供暖有关?
| P(K2≥kc) |
0.25 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
| Kc |
1.323 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
K2=
| |
非重度污染 |
重度污染 |
合计 |
| 供暖季 |
|
|
|
| 非供暖季 |
|
|
|
| 合计 |
|
|
100 |
(本小题满分14分)已知函数 (
( ).
).
(1)若 为函数
为函数 的极值点,求
的极值点,求 的值;
的值;
(2)若 ,
, 已知
已知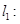
 ,
,
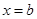 ,若直线
,若直线 、
、 及直线
及直线 与函数
与函数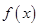 的图象所围成的封闭图形如阴影部分所示,求阴影面积
的图象所围成的封闭图形如阴影部分所示,求阴影面积 关于
关于 的函数
的函数 的最小值
的最小值 ;
; 证明不等式:
证明不等式: .
.
如图,在四棱锥 中,底面
中,底面 是矩形,
是矩形, 平面
平面 ,
, ,
, ,点
,点 是
是 的中点,点
的中点,点 是边
是边 上的任意一点.
上的任意一点.
(Ⅰ)当点 为
为 边的中点时,判断
边的中点时,判断 与平面
与平面 的位置关系,并加以证明;
的位置关系,并加以证明;
(Ⅱ)证明:无论点 在
在 边的何处,都有
边的何处,都有 ;
;
(Ⅲ)求三棱锥 的体积.
的体积.
选修4-5: 不等式选讲
设函数 .
.
(Ⅰ)解不等式 ;
;
(Ⅱ)若 ,使得
,使得 ,求实数
,求实数 的取值范围.
的取值范围.
21.
已知实数 为常数,函数
为常数,函数 .
.
(Ⅰ)若曲线 在
在 处的切线过点A
处的切线过点A ,求实数
,求实数 值;
值;
(Ⅱ)若函数 有两个极值点
有两个极值点 .
.
求证: ,②求证:
,②求证: .
.
已知函数 .
.
(I)求函数 的最小正周期;
的最小正周期;
(II)将函数 的图象向左平移
的图象向左平移 个单位,得到函数
个单位,得到函数 的图象.在
的图象.在 中,角A,B,C的对边分别为
中,角A,B,C的对边分别为 ,若
,若 ,求
,求 的面积.
的面积.
某省为了研究雾霾天气的治理,一课题组对省内24个城市进行了空气质量的调查,按地域特点把这些城市分成了甲、乙、丙三组.已知三组城市的个数分别为4,8,12,课题组用分层抽样的方法从中抽取6个城市进行空气质量的调查.
(I)求每组中抽取的城市的个数;
(II)从已抽取的6个城市中任抽两个城市,求两个城市不来自同一组的概率.
(本小题满分12分)已知等比数列 的前n项和为
的前n项和为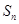 ,且满足
,且满足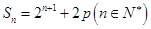 .
.
(I)求p的值及数列 的通项公式;
的通项公式;
(II)若数列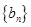 满足
满足 ,求数列
,求数列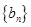 的前n项和
的前n项和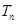 .
.
(本小题满分10分)在△ABC中, 分别是角A,B,C的对边.
分别是角A,B,C的对边.
(1)求证: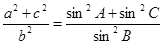 ;
;
(2)已知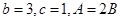 ,求
,求 的值.
的值.
(本小题满分13分)
如图,⊙O在平面 内,AB是⊙O的直径,
内,AB是⊙O的直径, 平面
平面 ,C为圆周上不同于A、B的任意一点,M,N,Q分别是PA,PC,PB的中点.
,C为圆周上不同于A、B的任意一点,M,N,Q分别是PA,PC,PB的中点.
(1)求证: 平面
平面 ;
;
(2)求证:平面 平面
平面 ;
;
(3)求证: 平面
平面 .
.
选修4—4:坐标系与参数方程(本小题满分10分)
已知极坐标系的极点在直角坐标系的原点,极轴与x轴的正半轴重合.曲线C的极坐标方程为 ,直线l的参数方程为
,直线l的参数方程为 (t为参数,t∈R).试在曲线C上求一点M,使它到直线l的距离最大.
(t为参数,t∈R).试在曲线C上求一点M,使它到直线l的距离最大.
(本小题满分14分)
如图,四边形 是正方形,△
是正方形,△ 与△
与△ 均是以
均是以 为直角顶点的等腰直角三角形,点
为直角顶点的等腰直角三角形,点 是
是 的中点,点
的中点,点 是边
是边 上的任意一点.
上的任意一点.
(1)求证: ;
;
(2)求二面角 的平面角的正弦值.
的平面角的正弦值.
试题篮
()