(本小题满分13分)在四棱锥 中,底面
中,底面 是正方形,
是正方形, 与
与 交于点
交于点 ,
, 底面
底面 ,
, 为
为 的中点.
的中点. 
(Ⅰ)求证: ∥平面
∥平面 ;
;
(Ⅱ)求证: ;
;
(Ⅲ)若 在线段
在线段 上是否存在点
上是否存在点 ,使
,使 平面
平面 ?
?
若存在,求出 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
(本小题满分13分)如图,港口 在港口
在港口 正东方
正东方 海里处,小岛
海里处,小岛 在港口
在港口 北偏东
北偏东 方向和港口
方向和港口 北偏西
北偏西 方向上,一艘科学考察船从港口O出发,沿北偏东
方向上,一艘科学考察船从港口O出发,沿北偏东 的
的 方向以每小时
方向以每小时 海里的速度驶离港口
海里的速度驶离港口 ,一艘快艇从港口B出发,以每小时
,一艘快艇从港口B出发,以每小时 海里的速度驶向小岛
海里的速度驶向小岛 ,在
,在 岛装运补给物资后给考察船送去,现两船同时出发,补给物资的装船时间需要
岛装运补给物资后给考察船送去,现两船同时出发,补给物资的装船时间需要 小时,问快艇驶离港口
小时,问快艇驶离港口 后最少要经过多少时间才能和考察船相遇?
后最少要经过多少时间才能和考察船相遇?
家政服务公司根据用户满意程度将本公司家政服务员分为两类,其中A类服务员12名,B类服务员 名
名
(1)若采用分层抽样的方法随机抽取20名家政服务员参加技术培训,抽取到B类服务员的人数是16, 求 的值
的值
(2)某客户来公司聘请2名家政服务员,但是由于公司人员安排已经接近饱和,只有3名A类家政服务员和2名B类家政服务员可供选择
①请列出该客户的所有可能选择的情况
②求该客户最终聘请的家政服务员中既有A类又有B类的概率
(本小题满分12分)口袋中装有除颜色,编号不同外,其余完全相同的2个红球,4个黑球.现从中同时取出3个球.
(Ⅰ)求恰有一个黑球的概率;
(Ⅱ)记取出红球的个数为随机变量 ,求
,求 的分布列和数学期望
的分布列和数学期望 .
.
(本小题满分10分)等差数列 中,
中, ,公差
,公差 且
且 成等比数列,前
成等比数列,前 项的和为
项的和为 .
.
(1)求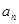 及
及 ;
;
(2)设 ,
,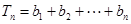 ,求
,求 .
.
(本小题满分14分)已知函数 ,其中
,其中 为自然对数的底数.
为自然对数的底数.
(Ⅰ)求曲线 在点
在点 处的切线方程;
处的切线方程;
(Ⅱ)若对任意 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(Ⅲ)试探究当 时,方程
时,方程 解的个数,并说明理由.
解的个数,并说明理由.
(本小题满分10分)已知命题 :方程
:方程 表示焦点在
表示焦点在 轴上的椭圆;命题
轴上的椭圆;命题 :点
:点 在圆
在圆 内.若
内.若 为真命题,
为真命题, 为假命题,试求实数
为假命题,试求实数 的取值范围.
的取值范围.
(本小题满分10分)设不等式 的解集为集合
的解集为集合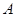 ,关于
,关于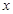 的不等式
的不等式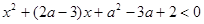 的解集为集合
的解集为集合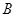 .
.
(1)若 ,求实数
,求实数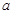 的取值范围;
的取值范围;
(2)若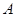 ∩
∩ ,求实数
,求实数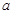 的取值范围.
的取值范围.
已知函数f(x)= 在
在 与x=1时都取得极值
与x=1时都取得极值
(1)求a、b的值与函数f(x)的单调区间
(2)若对xÎ[-1,2],不等式f(x)<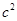 恒成立,求c的取值范围。
恒成立,求c的取值范围。
(本小题10分)在△ABC中,已知sinB= , cosA=
, cosA=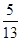 , 试求cosC的值.
, 试求cosC的值.
试题篮
()