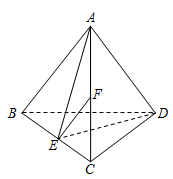
(本小题满分14分)如图,在四面体 中,
中, ,点
,点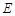 是
是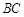 的中点,点
的中点,点 在线段
在线段 上,且
上,且 .
.
(1)若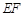 ∥平面
∥平面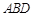 ,求实数
,求实数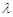 的值;
的值;
(2)求证:平面 平面
平面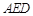 .
.
(本小题满分16分)设各项均为正数的数列 的前
的前 项和为
项和为 ,满足
,满足 ,且
,且 恰好是等比数列
恰好是等比数列 的
的
前三项.
(1)求数列 、
、 的通项公式;
的通项公式;
(2)记数列 的前
的前 项和为
项和为 ,若对任意的
,若对任意的 ,
, 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(本小题满分14分)已知函数 .
.
(1)求 的最小正周期;
的最小正周期;
(2)若将 的图像向右平移
的图像向右平移 个单位,得到函数
个单位,得到函数 的图像,求函数
的图像,求函数 在区间
在区间 上的最大值和最小值.
上的最大值和最小值.
如图,在平面直角坐标系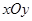 中,已知四边形
中,已知四边形 是等腰梯形,
是等腰梯形,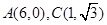 ,点
,点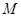 满足
满足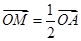 ,点
,点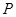 在线段
在线段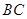 上运动(包括端点).
上运动(包括端点).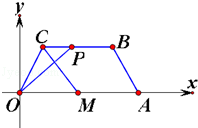
(1)求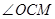 的余弦值;
的余弦值;
(2)是否存在实数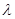 ,使
,使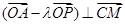 ,若存在,求出满足条件的实数
,若存在,求出满足条件的实数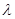 的取值范围,若不存在,请说明理由.
的取值范围,若不存在,请说明理由.
(本小题满分14分)某实验室某一天的温度(单位: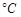 )随时间t(单位:h)的变化近似满足函数关系:
)随时间t(单位:h)的变化近似满足函数关系: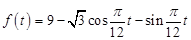 ,
,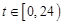 .
.
(1)求实验室这一天里,温度降低的时间段;
(2)若要求实验室温度不高于10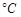 ,则在哪段时间实验室需要降温?
,则在哪段时间实验室需要降温?
(本小题满分12分)设函数 ,曲线
,曲线 在点P(1,0)处的切线斜率为2.
在点P(1,0)处的切线斜率为2.
(1)求a,b的值;
(2)证明: .
.
(本小题满分12分)某市公租房的房源位于 三个片区,设每位申请人只申请其中一个片区的房源,且申请其中任一个片区的房源是等可能的,求该市的任意4位申请人中:
三个片区,设每位申请人只申请其中一个片区的房源,且申请其中任一个片区的房源是等可能的,求该市的任意4位申请人中:
(1)恰有2人申请 片区房源的概率;
片区房源的概率;
(2)申请的房源所在片区的个数 的分布列和期望.
的分布列和期望.
(本小题满分12分)如图,已知点A(11,0), 函数 的图象上的动点P在x轴上的射影为H,且点H在点A的左侧.设
的图象上的动点P在x轴上的射影为H,且点H在点A的左侧.设 ,△APH的面积为
,△APH的面积为 .
.
(1)求函数 的解析式及
的解析式及 的取值范围;
的取值范围;
(2)求函数 的最大值.
的最大值.
有6名男医生,4名女医生.
(1)选3名男医生,2名女医生,让这5名医生到5个不同地区去巡回医疗,共有多少种不同方法?
(2)把10名医生分成两组,每组5人且每组都要有女医生,则有多少种不同分法?若将这两组医生分派到两地去,并且每组选出正副组长两人,又有多少种不同方案?
【原创】已知函数
(1)设 的零点
的零点 满足
满足 ,求
,求 的值;
的值;
(2)若 ,且
,且 对任意的
对任意的 1恒成立,求
1恒成立,求 的最大值.
的最大值.
已知 在区间
在区间 上是增函数,在区间
上是增函数,在区间 和
和 上是减函数,且
上是减函数,且
(1)求函数 的解析式.
的解析式.
(2)若在区间 上恒有
上恒有 ,求实数
,求实数 的取值范围.
的取值范围.
设函数 对任意实数x 、y都有
对任意实数x 、y都有 ,
,
(1)求 的值;
的值;
(2)若 ,求
,求 、
、 、
、 的值;
的值;
(3)在(2)的条件下,猜想
 的表达式,并用数学归纳法加以证明。
的表达式,并用数学归纳法加以证明。
试题篮
()