高中数学解答题

已知复数满足为实数（为虚数单位），且，求.

已知函数是奇函数。
（1）求实数a的值；
（2）判断函数在R上的单调性并用定义法证明；
（3）若函数的图像经过点，这对任意不等式≤恒成立，求实数m的范围。

已知二次函数的导函数的图像与直线平行，且在处取得极小值．设．
（1）若曲线上的点到点的距离的最小值为，求的值；
（2）如何取值时，函数存在零点，并求出零点．

定义：设分别为曲线和上的点，把两点距离的最小值称为曲线到的距离．
（1）求曲线到直线的距离；
（2）已知曲线到直线的距离为，求实数的值；
（3）求圆到曲线的距离．

已知函数．
(1)求的单调区间；
(2)当时，判断和的大小，并说明理由；
(3)求证：当时，关于的方程：在区间上总有两个不同的解．

已知函数 .
(1)若，求的单调区间及的最小值；
(2)若,求的单调区间；
(3)试比较与的大小,并证明你的结论.

某单位实行休年假制度三年来，名职工休年假的次数进行的调查统计结果如下表所示：

休假次数
人数

根据上表信息解答以下问题：
⑴从该单位任选两名职工，用表示这两人休年假次数之和，记“函数,在区间，上有且只有一个零点”为事件，求事件发生的概率；
⑵从该单位任选两名职工，用表示这两人休年假次数之差的绝对值，求随机变量的分布列及数学期望.

已知函数
（Ⅰ）求的最小正周期；
（Ⅱ）在中，角所对的边分别是若且，试判断的形状．

已知函数 $f\left(x\right)=\cos x·\cos \left(x-\frac{\mathrm{\pi }}{3}\right)$

（1）求 $f\left(\frac{2\mathrm{\pi }}{3}\right)$的值；
（2）求使 $f\left(x\right)<\frac{1}{4}$成立的 $x$的取值集合

已知函数 $f\left(x\right)=\sqrt{2}\cos (x-\frac{\pi }{12}),x\in R$．
(1) 求 $f\left(\frac{\pi }{3}\right)$的值；
(2) 若 $\cos \theta =\frac{3}{5},\theta \in (\frac{3\pi }{2},2\pi )$，求 $f(\theta -\frac{\pi }{6})$．

已知矩阵 $A=\left[\begin{array}{cc}-1& 0\\ 0& 2\end{array}\right]$， $B=\left[\begin{array}{cc}0& 2\\ 1& 6\end{array}\right]$，求矩阵 $A^{-1}B$.

已知 $a=(\cos \alpha ,\sin \alpha ),b=(\cos \beta ,\sin \beta ),0<\beta <\alpha <\pi$.
（1）若 $\left|a-b\right|=\sqrt{2}$，求证： $a\perp b$；
（2）设 $c\ne (0,1)$，若 $a+b=c$，求 $\alpha ,\beta$的值.

设椭圆 $\frac{x^2}{a^2}+\frac{y^2}{1-a^2}=1$的焦点在 $x$轴上.
（Ⅰ）若椭圆 $E$的焦距为1，求椭圆 $E$的方程；
（Ⅱ）设 $F_1,F_2$分别是椭圆的左、右焦点， $P$为椭圆 $E$上第一象限内的点，直线 $F_{2}P$交 $y$轴与点 $Q$，并且 $F_{1}P\perp F_{1}Q$，证明：当 $a$变化时，点 $P$在某定直线上.

已知 $\left\{a_n\right\}$是由非负整数组成的无穷数列，该数列前 $n$项的最大值记为 $A_n$，第n项之后各项 $a_{n+1}$， $a_{n+2}$…的最小值记为 $B_n$， $d_n=A_n-B_n$.
(1)若 $\left\{a_n\right\}$为2，1，4，3，2，1，4，3…，是一个周期为4的数列(即对任意 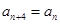$n\in N^{*}$， $a_{n+4}=a_n$)，写出 $d_1$， $d_2$， $d_3$， $d_4$的值；
(2)设d为非负整数，证明： $d_n=-d$( $n=1,2,3\dots$)的充分必要条件为{a_n}为公差为d的等差数列；
(3)证明：若 $a_1=2$， $d_n=1(n=1,2,3\dots )$，则 $\left\{a_n\right\}$的项只能是1或2，且有无穷多项为1.

如图，在三棱柱 $ABC-A_1{B}_1{C}_1$中， $A{A}_1{C}_{1}C$是边长为4的正方形.平面 $ABC\perp$平面 $A{A}_1{C}_{1}C$， $AB=3,BC=5$.

（Ⅰ）求证： $A{A}_1\perp$平面 $ABC$；
（Ⅱ）求二面角 $A_1-B{C}_1-B_1$的余弦值；
（Ⅲ）证明：在线段 $B{C}_1$存在点 $D$，使得 $AD\perp A_{1}B$，并求 $\frac{BD}{B{C}_1}$的值.