在平面直角坐标系xOy中,圆C的参数方程为 ,直线l经过点P(2,2),倾斜角
,直线l经过点P(2,2),倾斜角 。
。
(1)写出圆的标准方程和直线l的参数方程;
(2)设l与圆C相交于A、B两点,求 的值。
的值。
)袋中装有大小相同的黑球、白球和红球共10个。已知从袋中任意摸出1个球,得到黑球的概率是 ;从袋中任意摸出2个球,至少得到1个白球的概率是
;从袋中任意摸出2个球,至少得到1个白球的概率是
(1)求袋中各色球的个数;
(2)从袋中任意摸出3个球,记得到白球的个数为ξ,求随机变量ξ的分布列及数学期望Eξ和方差Dξ;
有4个不同的球,四个不同的盒子,把球全部放入盒内(结果用数字表示).
(1)共有多少种放法?
(2)恰有一个盒子不放球,有多少种放法?
(3)恰有一个盒内放2个球,有多少种放法?
(4)恰有两个盒不放球,有多少种放法?
若存在实常数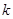 和
和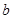 ,使得函数
,使得函数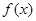 和
和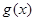 对其定义域上的任意实数
对其定义域上的任意实数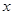 分别满足:
分别满足: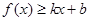 和
和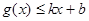 ,则称直线
,则称直线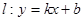 为
为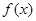 和
和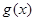 的“隔离直线”.已知
的“隔离直线”.已知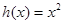 ,
,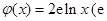 为自然对数的底数).
为自然对数的底数).
(Ⅰ)求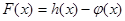 的极值;
的极值;
(Ⅱ)函数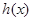 和
和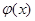 是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由.
是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由.
已知数列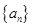 的前
的前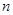 项和为
项和为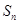 ,且对任意的
,且对任意的 都有
都有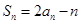 ,
,
(Ⅰ)求数列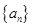 的前三项
的前三项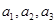 ;
;
(Ⅱ)猜想数列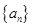 的通项公式
的通项公式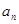 ,并用数学归纳法证明
,并用数学归纳法证明
已知曲线 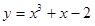 在点
在点 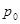 处的切线
处的切线 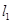 平行直线
平行直线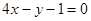 ,且点
,且点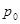 在第三象限.
在第三象限.
(Ⅰ)求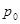 的坐标;
的坐标;
(Ⅱ)若直线 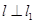 , 且
, 且  也过切点
也过切点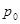 ,求直线
,求直线 的方程.
的方程.
如图,已知正方体 ,
,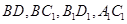 分别为各个面的对角线;
分别为各个面的对角线;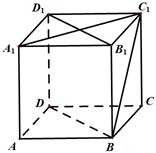
(1)求证: ;
;
(2)求异面直线 所成的角.
所成的角.
试题篮
()