高中数学解答题

已知两条直线，；
求为何值时，与（1）相交；（2）平行；（3）垂直.

求满足下列条件的直线方程：
（1）经过两条直线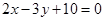和的交点，且平行于直线；
（2）经过两条直线和的交点，且垂直于直线.

设集合,函数.
(1)若且的最小值为1;求实数的值
(2)若,且,求的取值范围.

已知函数在处取得极值.
(1)求;
(2)设函数为R上的奇函数,求函数在区间上的极值.

已知圆M:与轴相切。
（1）求的值；
（2）求圆M在轴上截得的弦长；
（3）若点是直线上的动点，过点作直线与圆M相切，
为切点。求四边形面积的最小值。

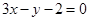已知四棱锥P－ABCD的三视图和直观图如下：

(1)求四棱锥P－ABCD的体积；
(2) 若E是侧棱PC上的动点，是否不论点E在何位置，都有BD⊥AE？证明你的结论．
(3) 若F是侧棱PA上的动点，证明：不论点F在何位置，都不可能有BF⊥平面PAD。

已知三角形ABC的顶点坐标分别为A，B，C；
（1）求直线AB方程的一般式；
（2）证明△ABC为直角三角形；
（3）求△ABC外接圆方程。

设数列前n项和，且.
（Ⅰ）试求数列的通项公式；
（Ⅱ）设，求数列的前项和

设函数。
（1）求的最大值及周期；
（2）若锐角满足，求的值.

设△的内角所对边的长分别为，且有。
（1）求角的大小；
（2) 若，，为的中点，求的长。

已知为锐角，，，求的值.

已知数列满足：，数列满足.
（1）若是等差数列，且求的值及的通项公式；
（2）若是公比为的等比数列，问是否存在正实数，使得数列为等比数列？若存在，求出的值；若不存在，请说明理由；
（3）若是等比数列，求的前项和（用n,表示）.

运货卡车以每小时千米的速度匀速行驶130千米（单位：千米/小时）．假设汽油的价格是每升6元，而汽车每小时耗油升，司机的工资是每小时30元．
（1）求这次行车总费用关于的表达式；
（2）当为何值时，这次行车的总费用最低，并求出最低费用的值．

已知在△ABC中， a、b、c分别为角A、B、C的对边，且
（1）若，试判断△ABC的形状；
（2）若a=，b+c=3，求b和c的值．

数列中，，，
（1）若数列为公差为11的等差数列，求
（2）若数列为以为首项的等比数列，求数列的前m项和