选修4 - 4:坐标系与参数方程
已知极坐标系的极点与直角坐标系的原点重合,极轴与 轴的正半轴重合.若曲线
轴的正半轴重合.若曲线 的极坐标方程为
的极坐标方程为 ,曲线
,曲线 的参数方程为
的参数方程为 (
( 为参数).
为参数).
(1)将 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(2)若 上的点
上的点 对应的参数为
对应的参数为 ,
, 为
为 上的动点,求
上的动点,求 的最小值。
的最小值。
已知函数 ,
, ,
, .
.
(1)若 ,求证:
,求证:
(ⅰ) 在
在 的单调减区间上也单调递减;
的单调减区间上也单调递减;
(ⅱ) 在
在 上恰有两个零点;
上恰有两个零点;
(2)若 ,记
,记 的两个零点为
的两个零点为 ,求证:
,求证: .
.
若数列 中不超过
中不超过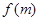 的项数恰为
的项数恰为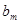 (
( ),则称数列
),则称数列 是数列
是数列 的生成数列,称相应的函数
的生成数列,称相应的函数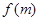 是数列
是数列 生成
生成 的控制函数.
的控制函数.
(1)已知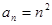 ,且
,且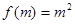 ,写出
,写出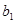 、
、 、
、 ;
;
(2)已知 ,且
,且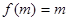 ,求
,求 的前
的前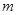 项和
项和 ;
;
(3)已知 ,且
,且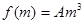 (
( ),若数列
),若数列 中,
中,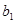 ,
, ,
, 是公差为
是公差为 (
( )的等差数列,且
)的等差数列,且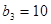 ,求
,求 的值及
的值及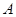 的值
的值
已知函数 (
( ),其中
),其中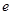 是自然对数的底数.
是自然对数的底数.
(1)当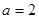 时,求
时,求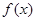 的极值;
的极值;
(2)若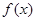 在
在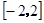 上是单调增函数,求
上是单调增函数,求 的取值范围;
的取值范围;
(3)当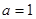 时,求整数
时,求整数 的所有值,使方程
的所有值,使方程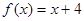 在
在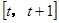 上有解.
上有解.
已知函数 (
( )的周期为
)的周期为 .
.
(1)当 时,求函数
时,求函数 的值域;
的值域;
(2)已知 的内角
的内角 ,
, ,
, 对应的边分别为
对应的边分别为 ,
, ,
, ,若
,若 ,且
,且 ,
, ,求
,求 的面积.
的面积.
如图,在直三棱柱 中,底面
中,底面 是直角三角形,
是直角三角形, ,点
,点 是棱
是棱 上一点,满足
上一点,满足 .
.
(1)若 ,求直线
,求直线 与平面
与平面 所成角的正弦值;
所成角的正弦值;
(2)若二面角 的正弦值为
的正弦值为 ,求
,求 的值.
的值.
如图,在四棱锥 中,已知底面
中,已知底面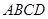 为矩形,
为矩形, 平面
平面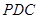 ,点
,点 为棱
为棱 的中点,求证:
的中点,求证:
(1) 平面
平面 ;
;
(2)平面 平面
平面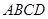 .
.
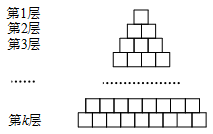
如图,由若干个小正方形组成的k层三角形图阵,第一层有1个小正方形,第二层有2个小正方形,依此类推,第k层有k个小正方形.除去最底下的一层,每个小正方形都放置在它下一层的两个小正方形之上.现对第k层的每个小正方形用数字进行标注,从左到右依次记为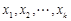 ,其中
,其中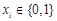 (
(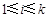 ),其它小正方形标注的数字是它下面两个小正方形标注的数字之和,依此规律,记第一层的小正方形标注的数字为
),其它小正方形标注的数字是它下面两个小正方形标注的数字之和,依此规律,记第一层的小正方形标注的数字为 .
.
(1)当k=4时,若要求 为2的倍数,则有多少种不同的标注方法?
为2的倍数,则有多少种不同的标注方法?
(2)当k=11时,若要求 为3的倍数,则有多少种不同的标注方法?
为3的倍数,则有多少种不同的标注方法?
一位网民在网上光顾某网店,经过一番浏览后,对该店铺中的 三种商品有购买意向.已知该网民购买
三种商品有购买意向.已知该网民购买 种商品的概率为
种商品的概率为 ,购买
,购买 种商品的概率为
种商品的概率为 ,购买
,购买 种商品的概率为
种商品的概率为 .假设该网民是否购买这三种商品相互独立.
.假设该网民是否购买这三种商品相互独立.
(1)求该网民至少购买2种商品的概率;
(2)用随机变量 表示该网民购买商品的种数,求
表示该网民购买商品的种数,求 的概率分布和数学期望.
的概率分布和数学期望.
在直角坐标系xOy中,已知曲线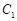 的参数方程是
的参数方程是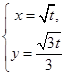
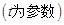 ,在以坐标原点O为极点,
,在以坐标原点O为极点, 轴的正半轴为极轴的极坐标系中,曲线
轴的正半轴为极轴的极坐标系中,曲线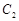 的极坐标方程是
的极坐标方程是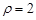 ,求曲线
,求曲线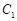 与
与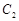 的交点在直角坐标系中的直角坐标.
的交点在直角坐标系中的直角坐标.
已知二阶矩阵M有特征值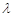 =3及对应的一个特征向量
=3及对应的一个特征向量 ,并且矩阵M对应的变换将点(-1,2)变换成(9,15),求矩阵M.
,并且矩阵M对应的变换将点(-1,2)变换成(9,15),求矩阵M.
试题篮
()