高中数学解答题

已知等比数列{a_n}的各项均为正数，且2a₁，成等差数列，a₂，，a₆成等比数列．
（1）求数列{a_n}的通项公式；
（2）设b_n=log₃，记S_n=，求S_n．

已知椭圆C：+=1（a＞b＞0）过点（1，），且长轴长等于4．
（Ⅰ）求椭圆C的方程；
（Ⅱ）F₁，F₂是椭圆C的两个焦点，⊙O是以F₁，F₂为直径的圆，直线l：y=kx+m与⊙O相切，并与椭圆C交于不同的两点A，B，若•=﹣，求k的值．

在数列{a_n}中，已知．
（1）求数列{a_n}的通项公式；
（2）求证：数列{b_n}是等差数列；
（3）设数列{c_n}满足c_n=a_n+b_n，求{c_n}的前n项和S_n．

已知函数f（x）=2sinωxcosωx﹣2sin²ωx+（ω＞0），直线x=x₁，x=x₂是函数y=f（x）的图象的任意两条对称轴，且|x₁﹣x₂|的最小值为．
（Ⅰ）求ω的值；
（Ⅱ）求函数f（x）的单调增区间；
（Ⅲ）若f（α）=，求sin（π﹣4α）的值．

设函数f（x）=x²（e^x﹣1）+ax³
（1）当时，求f（x）的单调区间；
（2）若当x≥0时，f（x）≥0恒成立，求a的取值范围．

设数列{a_n}满足当n＞1时，．
（1）求证：数列为等差数列；
（2）试问a₁a₂是否是数列{a_n}中的项．如果是，是第几项；如果不是，说明理由．

已知{a_n}的前n项和S_n，a_n＞0且a_n²+2a_n=4S_n+3
（1）求{a_n}的通项公式；
（2）若b_n=，求{b_n}的前n项和T_n．

如图，墙上有一壁画，最高点A离地面4米，最低点B离地面2米．观察者从距离墙x（x＞1）米，离地面高a（1≤a≤2）米的C处观赏该壁画，设观赏视角∠ACB=θ．

（1）若a=1.5，问：观察者离墙多远时，视角θ最大？
（2）若tanθ=，当a变化时，求x的取值范围．

已知函数
（Ⅰ）求函数f（x）的定义域
（Ⅱ）若，求cosα的值
（Ⅲ）在（Ⅱ）条件下，若α是第四象限角，求的值．

已知函数f（x）=x²﹣（a+2）x+alnx．
（1）当a=1时，求函数f（x）的极值；
（2）设定义在D上的函数y=g（x）在点P（x₀，y₀）处的切线方程为l：y=h（x）．当x≠x₀时，若＞0在D内恒成立，则称P为函数y=g（x）的“转点”．当a=8时，问函数y=f（x）是否存在“转点”？若存在，求出“转点”的横坐标；若不存在，请说明理由．

已知非零数列{a_n}满足a₁=1，a_na_n+1=a_n﹣2a_n+1（n∈N^*）．
（1）求证：数列是等比数列；
（2）若关于n的不等式＜m﹣3有解，求整数m的最小值；
（3）在数列中，是否存在首项、第r项、第s项（1＜r＜s≤6），使得这三项依次构成等差数列？若存在，求出所有的r、s；若不存在，请说明理由．

在△ABC中，角A，B，C的对边分别为a，b，c，向量=（cosC，sin），向量=（sin，cosC），且．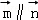
（1）求角C的大小；
（2）若a²=2b²+c²，求tanA的值．

在平面直角坐标系xOy中，已知向量=（2，0），=（0，1）．设向量，，其中0＜θ＜．
（1）若∥，且θ=，求实数k的值；
（2）若⊥，求实数k的最大值，并求取最大值时cosθ的值．

如图，AB是的⊙O直径，CB与⊙O相切于B，E为线段CB上一点，连接AC、AE分别交⊙O于D、G两点，连接DG交CB于点F．

（Ⅰ）求证：C、D、G、E四点共圆．
（Ⅱ）若F为EB的三等分点且靠近E，EG=1，GA=3，求线段CE的长．

已知数列{a_n}的前n项和为S_n，且a₁=．
（1）求{a_n}的通项公式；
（2）设b_n=n（2﹣S_n），n∈N^*，若b_n≤λ，n∈N^*恒成立，求实数λ的取值范围．
（3）设C_n=，T_n是数列{C_n}的前n项和，证明≤T_n＜1．