一个正方体的平面展开图及该正方体的直观图的示意图如图所示,在正方体中,设 的中点为 , 的中点为

(1)请将字母
标记在正方体相应的顶点处(不需说明理由)
(2)证明:直线
平面
(3)求二面角 的余弦值
某市
两所中学的学生组队参加辩论赛,
中学推荐3名男生,2名女生,
中学推荐了3名男生,4名女生,两校推荐的学生一起参加集训,由于集训后队员的水平相当,从参加集训的男生中随机抽取3人,女生中随机抽取3人组成代表队
(1)求
中学至少有1名学生入选代表队的概率.
(2)某场比赛前,从代表队的6名队员中随机抽取4人参赛,设
表示参赛的男生人数,求
得分布列和数学期望.
设数列
的前
项和
,且
成等差数列.
(1)求数列
的通项公式;
(2)记数列
的前
项和
,求得
成立的
的最小值.
已知数列
与
满足
.
(1)若
,且
,求数列
的通项公式;
(2)设
的第
项是最大项,即
,求证:数列
的第
项是最大项;
(3)设
,求
的取值范围,使得对任意
,且
.
已知椭圆
,过原点的两条直线
和
分别于椭圆交于
、
和
、
,设
的面积为
.
(1)设
,
,用
、
的坐标表示点
到直线
的距离,并证明
;
(2)设
,
,
,求
的值;
(3)设
与
的斜率之积为
,求
的值,使得无论
与
如何变动,面积
保持不变.
如图,
三地有直道相通,
千米,
千米,
千米.现甲、乙两警员同时从
地出发匀速前往
地,经过
小时,他们之间的距离为
(单位:千米).甲的路线是
,速度为5千米/小时,乙的路线是
,速度为8千米/小时.乙到达
地后原地等待.设
时乙到达
地.
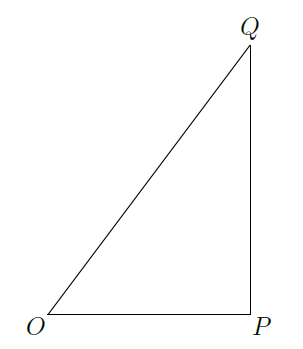
(1)求
与
的值;
(2)已知警员的对讲机的有效通话距离是3千米.当
时,求
的表达式,并判断
在
上得最大值是否超过3?说明理由.
已知函数
,其中
为实数.
(1)根据
的不同取值,判断函数
的奇偶性,并说明理由;
(2)若
,判断函数
在
上的单调性,并说明理由.
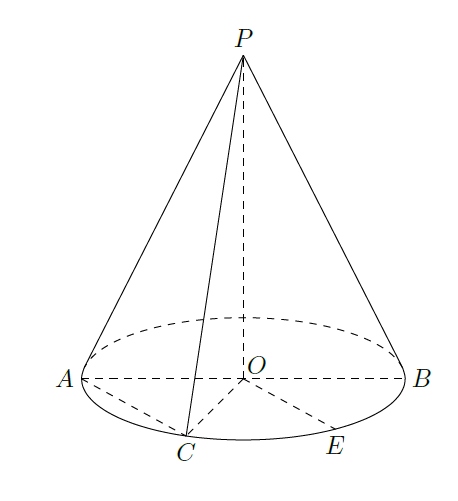
如图,圆锥的顶点为
,底面的一条直径为
,
为半圆弧
的中点,
为劣弧
的中点.已知
,求三棱锥
的体积,并求异面直线
与
所成角的大小.
对于定义域为
的函数
,若存在正常数
,使得
是以
为周期的函数,则称
为余弦周期函数,且称
为其余弦周期.已知
是以
为余弦周期的余弦周期函数,其值域为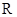 .设
单调递增,
,
.
.设
单调递增,
,
.
(1)验证
是以
为周期的余弦周期函数;
(2)设
.证明对任意
,存在
,使得
;
(3)证明:"
为
在
上得解"的充要条件是"
为方程
在
上有解",并证明对任意
都有
.
已知数列
与
满足
.
(1)若
,且
,求数列
的通项公式;
(2)设
的第
项是最大项,即
,求证:数列
的第
项是最大项;
(3)设
,求
的取值范围,使得
有最大值
与最小值
,且
.
已知椭圆
,过原点的两条直线
和
分别于椭圆交于
和
,记得到的平行四边形
的面积为
.
(1)设
,用
的坐标表示点
到直线
的距离,并证明
;
(2)设
与
的斜率之积为
,求面积
的值.
如图,
三地有直道相通,
千米,
千米,
千米.现甲、乙两警员同时从
地出发匀速前往
地,经过
小时,他们之间的距离为
(单位:千米).甲的路线是
,速度为5千米/小时,乙的路线是
,速度为8千米/小时.乙到达
地后原地等待.设
时乙到达
地.

(1)求
与
的值;
(2)已知警员的对讲机的有效通话距离是3千米.当
时,求
的表达式,并判断
在
上得最大值是否超过3?说明理由.
试题篮
()