已知数列是递增的等比数列,且
.
(Ⅰ)求数列的通项公式;
(Ⅱ)设为数列
的前
项和,
,求数列
的前
项和
.
某企业为了解下属某部门对本企业职工的服务情况,随机访问50名职工,根据这50名职工对该部门的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为
,
,...
,
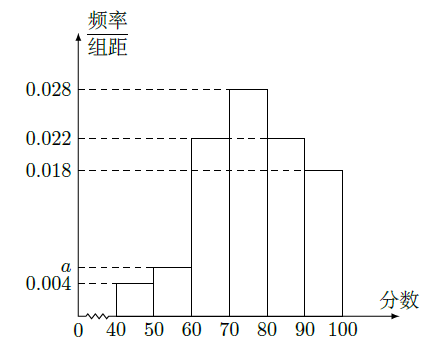
(Ⅰ)求频率分布图中
的值;
(Ⅱ)估计该企业的职工对该部门评分不低于80的概率;
(Ⅲ)从评分在
的受访职工中,随机抽取2人,求此2人评分都在
的概率.
设函数.
(Ⅰ)讨论函数在
内的单调性并判断有无极值,有极值时求出极值;
(Ⅱ)记,求函数
在
(Ⅲ)在(Ⅱ)中,取,求
满足
时的最大值.
设椭圆的方程为
,点
为坐标原点,点
的坐标为
,点
的坐标为
,点
在线段
上,满足
,直线
的斜率为
.
(Ⅰ)求的离心率
;
(Ⅱ)设点的坐标为
,
为线段
的中点,点N关于直线
的对称点的纵坐标为
,求
的方程.
如图所示,在多面体 ,四边形 , 均为正方形, 为 的中点,过 的平面交 于 .
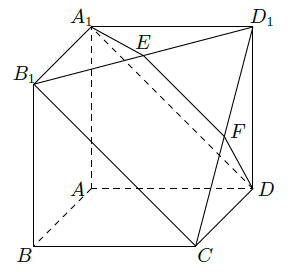
(Ⅰ)证明:
;
(Ⅱ)求二面角
余弦值.
设
,
是曲线
在点
处的切线与
轴交点的横坐标.
(Ⅰ)求数列
的通项公式;
(Ⅱ)记
,证明
.
已知2件次品和3件正品放在一起,现需要通过检测将其区分,每次随机检测一件产品,检测后不放回,直到检测出2件次品或者检测出3件正品时检测结束.
(Ⅰ)求第一次检测出的是次品且第二次检测出的是正品的概率;
(Ⅱ)已知每检测一件产品需要费用100元,设X表示直到检测出2件次品或者检测出3件正品时所需要的检测费用(单位:元),求的分布列和均值(数学期望).
试题篮
()