某商场举行有奖促销活动,顾客购买一定金额的商品后即可抽奖,抽奖方法是:从装有2个红球和1个白球
的甲箱与装有2个红球
和2个白球
的乙箱中,各随机摸出1个球,若摸出的2个球都是红球则中奖,否则不中奖。
(Ⅰ)用球的标号列出所有可能的摸出结果;
(Ⅱ)有人认为:两个箱子中的红球比白球多,所以中奖的概率大于不中奖的概率,你认为正确吗?请说明理由。
已知,函数
,记
为
的从小到大的第
(
)个极值点,证明:
(1)数列是等比数列
(2)若,则对一切
,
恒成立.
已知抛物线
的焦点
也是椭圆
的一个焦点,
与
的公共弦的长为
.
(1)求
的方程;
(2)过点
的直线
与
相交于
两点,与
相交于
两点,且
与
同向
(ⅰ)若
,求直线
的斜率
(ⅱ)设
在点
处的切线与
轴的交点为
,证明:直线
绕点
旋转时,
总是钝角三角形
如图,已知四棱台
上、下底面分别是边长为3和6的正方形,
,且
底面
,点
分别在棱
上.

(1)若
是
的中点,证明:
;
(2)若
平面
,二面角
的余弦值为
,求四面体
的体积.
某商场举行有奖促销活动,顾客购买一定金额商品后即可抽奖,每次抽奖都从装有4个红球、6个白球的甲箱和装有5个红球、5个白球的乙箱中,各随机摸出1个球,在摸出的2个球中,若都是红球,则获一等奖;若只有1个红球,则获二等奖;若没有红球,则不获奖.
(1)求顾客抽奖1次能获奖的概率;
(2)若某顾客有3次抽奖机会,记该顾客在3次抽奖中获一等奖的次数为,求
的分布列和数学期望.
已知直线
(
为参数),以坐标原点为极点,
轴的正半轴为极轴建立极坐标系,曲线
的极坐标方程为
.
(1)将曲线
的极坐标方程化为直角坐标方程;
(2)设点
的直角坐标为
,直线
与曲线
的交点为
,求
的值.
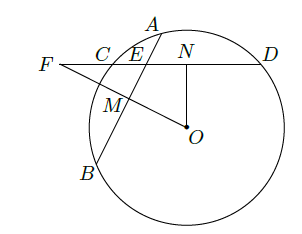
如图,在圆
中,相交于点
的两弦
,
的中点分别是
,
,直线
与直线
相交于点
,证明:
(1)
;
(2)
一种画椭圆的工具如图①所示.
是滑槽
的中点,短杆
可绕
转动,长杆
通过
处铰链与
连接,
上的栓子
可沿滑槽
滑动,且
,
.当栓子
在滑槽
内作往复运动时,带动
绕
转动,
处的笔尖画出的椭圆记为
.以
为原点,
所在的直线为
轴建立如图②所示的平面直角坐标系.

(Ⅰ)求椭圆
的方程;
(Ⅱ)设动直线
与两定直线
和
分别交于
两点.若直线
总与椭圆
有且只有一个公共点,试探究:
的面积是否存在最小值?若存在,求出该最小值;若不存在,说明理由.
设函数的定义域均为
,且
是奇函数,
是偶函数,
,其中
为自然对数的底数.
(Ⅰ)求的解析式,并证明:当
时,
;
(Ⅱ)设,证明:当
时,
.
《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑. 在如图所示的阳马
中,侧棱
底面
,且
,点
是
的中点,连接
.

(Ⅰ)证明:
平面
. 试判断四面体
是否为鳖臑,若是,写出其每个面的直角(只需写出结论);若不是,请说明理由;
(Ⅱ)记阳马
的体积为
,四面体
的体积为
,求
的值.
设等差数列
的公差为
,前
项和为
,等比数列
的公比为
.已知
.
(Ⅰ)求数列
,
的通项公式;
(Ⅱ)当
时,记
,求数列
的前
项和
.
试题篮
()