定义:如图1,平面上两条直线AB、CD相交于点O,对于平面内任意一点M,点M到直线AB、CD的距离分别为p、q,则称有序实数对(p,q)是点M的“距离坐标”.根据上述定义,“距离坐标”为(0,0)点有1个,即点O.
(1)“距离坐标”为(1,0)点有 个;
(2)如图2,若点M在过点O且与直线CD垂直的直线l上时,点M的“距离坐标”为(p,q),且∠BOD=120°.请画出图形,并直接写出p,q的关系式;
(3)如图3,点M的“距离坐标”为(1,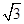 ),且∠AOB=30°,求OM的长.
),且∠AOB=30°,求OM的长.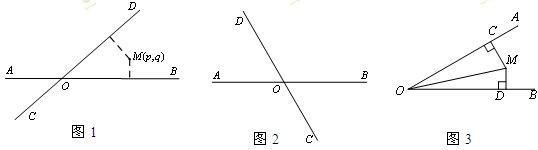
某海域有A,B两个港口,B港口在A港口北偏西30°方向上,距A港口60海里,有一艘船从A港口出发,沿东北方向行驶一段距离后,到达位于B港口南偏东75°方向的C处,求该船与B港口之间的距离即CB的长(结果保留根号).
已知抛物线 的图象如图所示,则下列结论:①
的图象如图所示,则下列结论:① >0;
>0;
② ; ③
; ③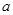 <
< ; ④
; ④ >1.其中正确的结论是 ( )
>1.其中正确的结论是 ( )
| A.①② | B.②③ | C.③④ | D.②④ |
已知数轴上的点A,B对应的数分别是x,y,且|x+100|+(y﹣200)2=0,点P为数轴上从原点出发的一个动点,速度为30单位长度/秒.
(1)求点A,B两点之间的距离;
(2)若点A向右运动,速度为10单位长度/秒,点B向左运动,速度为20单位长度/秒,点A,B和P三点同时开始运动,点P先向右运动,遇到点B后立即掉后向左运动,遇到点A再立即掉头向右运动,如此往返,当A,B两点相距30个单位长度时,点P立即停止运动,求此时点P移动的路程为多少个单位长度?
(3)若点A,B,P三个点都向右运动,点A,B的速度分别为10单位长度/秒,20单位长度/秒,点M、N分别是AP、OB的中点,设运动的时间为t(0<t<10),在运动过程中① 的值不变;②
的值不变;②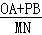 的值不变,可以证明,只有一个结论是正确的,请你找出正确的结论并求值.
的值不变,可以证明,只有一个结论是正确的,请你找出正确的结论并求值.
如图,在平面直角坐标系中,点M是第一象限内一点,过M的直线分别交x轴,y轴的正半轴于A,B两点,且M是AB的中点.以OM为直径的⊙P分别交x轴,y轴于C,D两点,交直线AB于点E(位于点M右下方),连结DE交OM于点K.
(1)若点M的坐标为(3,4),
①求A,B两点的坐标;
②求ME的长.
(2)若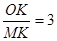 ,求∠OBA的度数.
,求∠OBA的度数.
(3)设tan∠OBA=x(0<x<1),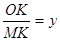 ,直接写出y关于x的函数解析式.
,直接写出y关于x的函数解析式.
亚奥理事会于2015年9月16日在土库曼斯坦阿什哈巴德举行第34届代表大会,并在会上投票选出2022年第19届亚运会举办城市为杭州.5个城市的国际标准时间(单位:时)在数轴上表示如图所示,那么北京时间2015年9月16日20时应是( )

| A.伦敦时间2015年9月16日11时 |
| B.巴黎时间2015年9月16日13时 |
| C.智利时间2015年9月16日5时 |
| D.曼谷时间2015年9月16日18时 |
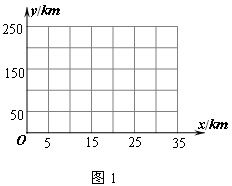
如图1,A,B,C为三个超市.在A通往C的道路(粗实线部分)上有一D点,D与B有道路(细实线部分)相通这.A与D,D与C,D与B之间的路程分别为25㎞,10㎞,5㎞.现计划在A通往C的道路上建一个配货中心H,每天有一辆货车只为这三个超市送货.该货车每于从H出发,单独为A送货1次,为B送货1次,为C送货2次.货车每次仅能给一家超市送货,每次送货后均返回配货中心H.设H到A的路程为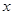 ㎞,这辆货车每天行驶的路程为
㎞,这辆货车每天行驶的路程为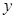 ㎞.
㎞.

(1)用含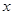 的代数式填空:当0≤
的代数式填空:当0≤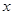 ≤25时货车从H到A往返1次的路程为2
≤25时货车从H到A往返1次的路程为2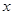 ㎞,货车从H到B往返1次的路程为 ㎞;货车从H到C往返2次的路程为 ㎞;这辆货车每天行驶的路程
㎞,货车从H到B往返1次的路程为 ㎞;货车从H到C往返2次的路程为 ㎞;这辆货车每天行驶的路程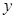 = ;当25<
= ;当25<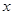 ≤35时,这辆货车每天行驶的路程
≤35时,这辆货车每天行驶的路程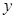 = ;
= ;
(2)请在图2中画出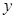 与
与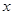 (0≤
(0≤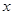 ≤35)的函数图象;
≤35)的函数图象;
(3)配货中心H建在哪段,这辆货车每天行驶的路程最短?
(11·贺州)如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1
次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),……,
按这样的运动规律,经过第2011次运动后,动点P的坐标是_ ▲ .
阅读与理解
在平面直角坐标系xoy中,点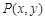 经过
经过 变换得到点
变换得到点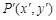 ,该变换记为
,该变换记为 ,其中
,其中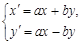
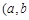 为常数
为常数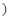 .
.
例如,当 ,且
,且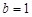 时,
时, .
.
(1) 当 ,且
,且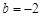 时,
时,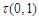 = ;
= ;
(2) 若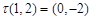 ,则
,则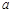 = ,
= ,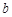 = ;
= ;
(3) 设点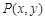 是直线
是直线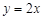 上的任意一点,点
上的任意一点,点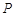 经过变换
经过变换 得到点
得到点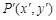 .若点
.若点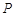 与点
与点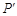 关于原点对称,求
关于原点对称,求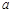 和
和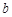 的值.
的值.
如图,某大楼的顶部树有一块广告牌CD,小明在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度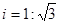 ,AB=10米,AE=15米.
,AB=10米,AE=15米.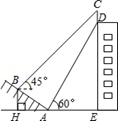
(1)求点B距水平面AE的高度BH;
(2)求广告牌CD的高度.
(测角器的高度忽略不计,结果精确到0.1米.参考数据: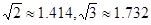 )
)
如图,在△ABC中,AB=AC=1,点D,E在直线BC上运动.设BD=x,CE=y.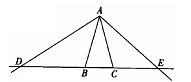
(l)如果∠BAC=300,∠DAE=l050,试确定y与x之间的函数关系式;
(2)如果∠BAC=α,∠DAE=β,当α,β满足怎样的关系时,(l)中y与x之间的函数关系式还成立?试说明理由.
如图,第(1)个多边形由正三角形“扩展”而来,边数记为 ,第(2)个多边形由正方形 “扩展”而来,边数记为
,第(2)个多边形由正方形 “扩展”而来,边数记为 ,…,依此类推,由正
,…,依此类推,由正 边形“扩展”而来的多边形的边数记为
边形“扩展”而来的多边形的边数记为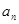 (n≥3).则
(n≥3).则 的值是 ,当
的值是 ,当 的结果是
的结果是 时,n的值 .
时,n的值 .
试题篮
()