如图所示,在直线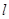 上有若干个点
上有若干个点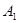 、
、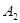 、…、
、…、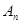 ,每相邻两点之间的距离都为1,点
,每相邻两点之间的距离都为1,点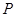 是线段
是线段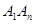 上的一个动点.
上的一个动点.
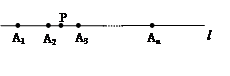
(1)当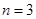 时,当点
时,当点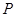 在点______(填
在点______(填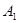 、
、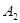 或
或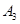 )的位置时,点
)的位置时,点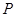 分别到点
分别到点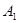 、
、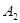 、
、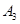 的距离之和最小;
的距离之和最小;
(2)当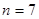 时,则点
时,则点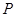 分别到点
分别到点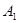 、
、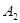 、…、
、…、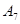 的距离之和的最小值是_________
的距离之和的最小值是_________
在数轴上表示下列各数,并用“<”号连接:
-(-5),-|-2.5|,- ,
, .
.
如图,在数轴上(未标出原点及单位长度),点A是线段BC的中点.已知点A、B、C所对应的三个数a、b、c之积是负数,这三个数之和与其中一个数相等,请直接写出求 、
、 的值.
的值.

答: 的值是 ,
的值是 , 的值是 .
的值是 .
有理数x、y在数轴上对应点如图所示:
(1)在数轴上表示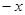 、
、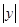 ;
;
(2)试把x、y、0、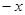 、
、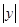 这五个数从小到大用“<”号连接;
这五个数从小到大用“<”号连接;
(3)化简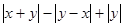 .
.
如图,在数轴上,点 、 分别表示数1、 .
(1)求 的取值范围;
(2)数轴上表示数 的点应落在 .
.点 的左边 .线段 上 .点 的右边

数和形是数学的两个主要研究对象,我们经常运用数形结合、数形转化的方法解决一些数学问题.下面我们来探究“由数思形,以形助数”的方法在解决代数问题中的应用.
探究一:求不等式 的解集
(1)探究 的几何意义
如图①,在以 为原点的数轴上,设点 对应的数是 ,由绝对值的定义可知,点 与点 的距离为 ,可记为 .将线段 向右平移1个单位得到线段 ,此时点 对应的数是 ,点 对应的数是1.因为 ,所以 .因此, 的几何意义可以理解为数轴上 所对应的点 与1所对应的点 之间的距离 .
(2)求方程 的解
因为数轴上3和 所对应的点与1所对应的点之间的距离都为2,所以方程的解为3, .
(3)求不等式 的解集
因为 表示数轴上 所对应的点与1所对应的点之间的距离,所以求不等式解集就转化为求这个距离小于2的点对应的数 的范围.
请在图②的数轴上表示 的解集,并写出这个解集.
探究二:探究 的几何意义
(1)探究 的几何意义
如图③,在直角坐标系中,设点 的坐标为 ,过 作 轴于 ,作 轴于 ,则 点坐标为 , 点坐标为 , , ,在 中, ,则 ,因此, 的几何意义可以理解为点 与点 之间的距离 .
(2)探究 的几何意义
如图④,在直角坐标系中,设点 的坐标为 ,由探究二(1)可知, ,将线段 先向右平移1个单位,再向上平移5个单位,得到线段 ,此时点 的坐标为 ,点 的坐标为 ,因为 ,所以 ,因此 的几何意义可以理解为点 与点 之间的距离 .
(3)探究 的几何意义
请仿照探究二(2)的方法,在图⑤中画出图形,并写出探究过程.
(4) 的几何意义可以理解为: .
拓展应用:
(1) 的几何意义可以理解为:点 与点 的距离和点 与点 (填写坐标)的距离之和.
(2) 的最小值为 (直接写出结果)

已知数轴上有A、B、C三点,分别代表﹣24,﹣10,10,两只电子蚂蚁甲、乙分别从A、C两点同时相向而行,甲的速度为4个单位/秒,乙的速度为6个单位/秒.
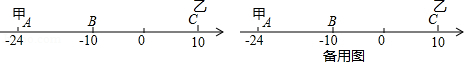
(1)甲、乙多少秒后相遇?
(2)甲出发多少秒后,甲到A、B、C三点的距离和为40个单位?
(3)当甲到A、B、C三点的距离和为40个单位时,甲调头返回,当甲、乙在数轴上再次相遇时,相遇点表示的数是 .
如图1,已知数轴上有三点A、B、C,AB=60,点A对应的数是40.
(1)若 ,求点C到原点的距离;
,求点C到原点的距离;
(2)如图2,在(1)的条件下,动点P、Q两点同时从C、A出发向右运动,同时动点R从点A向左运动,已知点P的速度是点R的速度的3倍,点Q的速度是点R的速度2倍少5个单位长度/秒.经过5秒,点P、Q之间的距离与点Q、R之间的距离相等,求动点Q的速度;
(3)如图3,在(1)的条件下,O表示原点,动点P、T分别从C、O两点同时出发向左运动,同时动点R从点A出发向右运动,点P、T、R的速度分别为5个单位长度/秒、1个单位长度/秒、2个单位长度/秒,在运动过程中,如果点M为线段PT的中点,点N为线段OR的中点.请问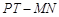 的值是否会发生变化?若不变,请求出相应的数值;若变化,请说明理由.
的值是否会发生变化?若不变,请求出相应的数值;若变化,请说明理由.
试题篮
()