若M( ,y1)、N(
,y1)、N( ,y2)、P(
,y2)、P( ,y3)三点都在函数
,y3)三点都在函数 (
( )的图象上,则yl、y2、y3的大小关系是( )
)的图象上,则yl、y2、y3的大小关系是( )
| A.y2>y3>y1 | B.y2>y1>y3 | C.y3>y1>y2 | D.y3>y2>y1 |
如图,在直角坐标平面内,点 与原点
与原点 的距离
的距离 ,线段
,线段 与
与 轴正半轴的夹角为
轴正半轴的夹角为 ,且
,且 ,则点
,则点 的坐标是( ).
的坐标是( ). 
| A.(2,3); | B.(2, ); ); |
C.( ,2); ,2); |
D.(2, ). ). |
图为一位旅行者在早晨8时从城市出发到郊外所走的路程S(单位:千米)与时间t(单位:时)的变量关系的图象。根据图象回答问题:
(1)在这个变化过程中,自变量是 ,因变量是 。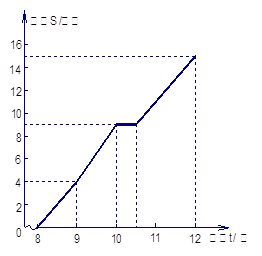
(2)9时,10时,12时所走的路程分别是多少?
(3)他休息了多长时间?
(4)他从休息后直至到达目的地这段时间的平均速度是多少?
已知变量y+1与(x-1)成反比例,且当x=2时,y=0.
(1)求y与x的函数关系式; (2)若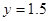 ,求此时的x值.
,求此时的x值.
如图,有一种动画程序,屏幕上正方形区域ABCD表示黑色物体甲.已知A (1,1),B (2,1),C (2,2),D (1,2),用信号枪沿直线y =" 2x" + b发射信号,当信号遇到区域甲(正方形ABCD)时,甲由黑变白.则b的取值范围为 时,甲能由黑变白.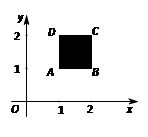
若点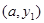 、
、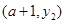 在直线
在直线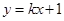 上,且
上,且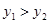 ,则该直线所经过的象限是
,则该直线所经过的象限是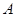 第一、二、三象限
第一、二、三象限  第一、二、四象限
第一、二、四象限  第二、三、四象限
第二、三、四象限  第一、三、四象限
第一、三、四象限
在平面直角坐标系中,点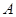 和点
和点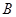 关于原点对称,已知点
关于原点对称,已知点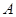 的坐标为(
的坐标为(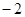 ,
,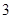 ),那么点
),那么点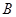 的坐标为( )
的坐标为( )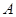 .(
.(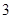 ,
,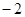 );
); 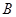 .(
.(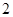 ,
,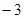 );
);  .(
.(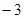 ,
,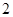 );
); 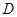 .(
.(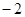 ,
,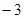 ).
).
已知, ,
,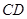 是
是 的平分线,点
的平分线,点 在
在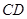 上,
上, .将三角板的直角顶点放置在点
.将三角板的直角顶点放置在点 处,绕着点
处,绕着点 旋转,三角板的一条直角边与射线
旋转,三角板的一条直角边与射线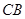 交于点
交于点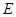 ,另一条直角边与直线
,另一条直角边与直线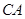 、直线分别交于点
、直线分别交于点 、点
、点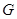 .
.
(1)如图,当点 在射线
在射线 上时,
上时,
①求证: 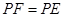 ;
;
②设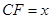 ,
,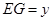 ,求
,求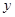 与
与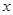 的函数解析式并写出函数的定义域;
的函数解析式并写出函数的定义域;
(2)连结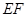 ,当△
,当△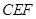 与△
与△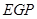 似时,求
似时,求 的长.
的长.
在平面直角坐标系中,已知A(1,1),B(3,3),则在x轴上存在一点C,C到到A、B的距离和最小,此时C的坐标为 .
打开某洗衣机开关,在(洗衣机内无水)洗涤衣服时,洗衣机经历了进水、清洗、排水、脱水四个连续过程,其中进水、清洗、排水时洗衣机中的水量y(升)与时间x(分钟)之间满足某种函数关系,其函数图象大致为( )
试题篮
()