初中数学非负数的性质：算术平方根解答题

将－2.5，，2，0，在数轴上表示出来，并用“＜”把他们连接起来

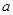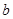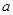
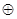
定义运算：对于任意实数、，都有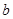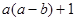＝，等式右边是通常的加法、减法、及乘法运算，比如：2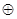5＝2×（2－5）+1＝2×（－3）+1＝－6+1＝－5．若3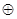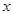的值小于13，求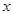的取值范围，并在如图所示的数轴上表示出来．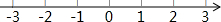

某股民在上周星期五买进某种股票1000股，每股10元，星期六，星期天股市不交易，下表是本周每日该股票的涨跌情况（单位：元）

星期	一	二	三	四	五
每股涨跌	+0．3	+0．1	﹣0．2	﹣0．5	+0．2

 
（1）本周星期五收盘时，每股是多少元？
（2）已知买进股票时需付买入成交额1．5%的手续费，卖出股票时需付卖出成交额1．5%的手续费和卖出成交额1%的交易费，如果在本周五收盘时将全部股票一次性地卖出，那么该股民的收益情况如何？

【背景知识】
数轴是初中数学的一个重要工具．利用数轴可以将数与形完美的结合．研究数轴我们发现了许多重要的规律：数轴上点、点表示的数为、，则，两点之间的距离，若，则可简化为；线段的中点表示的数为．
【问题情境】
已知数轴上有、两点，分别表示的数为，，点以每秒个单位的速度沿数轴向右匀速运动，点以每秒个单位向左匀速运动．设运动时间为秒（）．

【综合运用】
（1）运动开始前，、两点的距离为     ；线段的中点所表示的数     ．
（2）点运动秒后所在位置的点表示的数为     ；点运动秒后所在位置的点表示的数为     ；（用含的代数式表示）
（3）它们按上述方式运动，、两点经过多少秒会相遇，相遇点所表示的数是什么？
（4）若，按上述方式继续运动下去，线段的中点能否与原点重合，若能，求出运动时间，并直接写出中点的运动方向和运动速度；若不能，请说明理由．（当，两点重合，则中点也与， 两点重合）

（1）计算           
（2）解不等式：

已知一次函数的图像与 轴、轴分别相交于点A、B，点P在该函数图像上， P到轴、轴的距离分别为、。

（1）当P为线段AB的中点时，求的值；
（2）直接写出的范围，并求当时点P的坐标；
（3）若在线段AB 上存在无数个P点，使（为常数）， 求的值.

实数a、b在数轴上的位置如图所示，化简﹣（|a﹣b|﹣﹣），写出一个满足条件的a值，并求出此时代数式的值．

一个病人每天下午需要测量血压，下表为病人周一到周五收缩压的变化情况，该病上周日的收缩压力为160单位。

时间	周一	周二	周三	周四	周五
收缩压的变化与前一天相比较	+30	-20	+17	+18	-20

 
（1）本周哪一天血压最高？哪一天最低？（请用所学知识解释说明）
（2）与上周日相比，病人周五的血压是上升了还是下降了？

【原创】实数a,b,c在数轴上的位置如图所示，化简-|a+b|-|b+c|=

（1）画出数轴，并用数轴上的点表示下列各数：
-5，2.5，3，-，0，-3，3．
（2）用“＜”号把各数从小到大连起来：

（本题4分）把下列各数-1²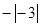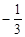，，，+（+2），在数轴上表示出来，并用“＞”把他们连接起来．

（本题4分）把下列各数填入表示它所在的数集的大括号：
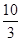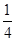－2．4，3，2．008，－，1，－，0，－（－2．28），π，－|－4|
正数集合：{                                 …}；
负有理数集合：{                             …}；
整数集合：{                                …}；
负分数集合：{                              …}．

一辆货车从百货大楼出发负责送货，向东走了4千米到达小明家，继续向东走了1.5千米到达小红家，然后向西走了8.5千米到达小刚家，最后返回百货大楼．

（1）以百货大楼为原点，向东为正方向，1个单位长度表示1千米，请你在数轴上标出小明．小红．小刚家的位置．（小明家用点A表示，小红家用点B表示，小刚家用点C表示）
（2）小明家与小刚家相距多远？
（3）若货车每千米耗油0.5升，那么这辆货车此次送货共耗油多少升？

（本题10分）2013年第23号台风“菲特”给浙江省带来了严重的影响。强降雨导致多处河水猛涨，城区受淹。西湖也出现了罕见的水满现象。在10月7日凌晨，西湖达到警戒水位7．3 m ．下表记录了这几日西湖水位的变化情况：（把10月7日凌晨的水位记作0，此后，正数表示比前一观察时间上升，负数表示下降）。

时间	10月7日凌晨	10月7日15时	10月8日、	10月9日 8时	10月10日12时	10月10日15点
水位变化 （米）	0	+0．15	+0．20	-0．13	-0．26	-0．03

 
（1）10月9日8时西湖水位是多少？
（2）这几日西湖水位最高值是多少？超过警戒水位多少米？
（3）从表中可以得知什么时候开始西湖水位已恢复到警戒水位之下？

某公路检修队乘车从A地出发，在南北走向的公路上检修道路，规定向南走为正，向北走为负，从出发到收工时所行驶的路程记录如下（单位：千米）：+3，－9，+4，+6，－10，+5，－3，+14.
（1）问收工时，检修队在A地哪边，距A地多远?
（2）问从出发到收工时，汽车共行驶多少千米?
（3）在汽车行驶过程中，若每行驶l千米耗油0.15升.公路检修队检查到第四处的加油站时，刚好油用完，加油时发现比上次加油时油价下跌了0.2元/升.检修队从A地出发到回到A地，共用油费64.98元.问此次加油的油价是每升多少元?