如图,在平面直角坐标系中,直线 与函数 的图象交于点 , .过点 作 平行于 轴交 轴于点 ,在 轴负半轴上取一点 ,使 ,且 的面积是6,连接 .
(1)求 , , 的值;
(2)求 的面积.

在平面直角坐标系 中,函数 的图象 经过点 ,直线 与图象 交于点 ,与 轴交于点 .
(1)求 的值;
(2)横、纵坐标都是整数的点叫做整点.记图象 在点 , 之间的部分与线段 , , 围成的区域(不含边界)为 .
①当 时,直接写出区域 内的整点个数;
②若区域 内恰有4个整点,结合函数图象,求 的取值范围.
如图,在平面直角坐标系 中,函数 的图象与直线 交于点 .
(1)求 、 的值;
(2)已知点 , ,过点 作平行于 轴的直线,交直线 于点 ,过点 作平行于 轴的直线,交函数 的图象于点 .
①当 时,判断线段 与 的数量关系,并说明理由;
②若 ,结合函数的图象,直接写出 的取值范围.

如图, 正比例函数 与反比例函数 的图象有一个交点 , 轴于点 . 平移直线 ,使其经过点 ,得到直线 ,则直线 对应的函数表达式是 .
如图,一次函数 的图象分别与反比例函数 的图象在第一象限交于点 ,与 轴的负半轴交于点 ,且 .
(1)求函数 和 的表达式;
(2)已知点 ,试在该一次函数图象上确定一点 ,使得 ,求此时点 的坐标.

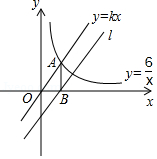
如图,一次函数y=kx+1(k≠0)与反比例函数y= (m≠0)的图象有公共点A(1,2).直线l⊥x轴于点N(3,0),与一次函数和反比例函数的图象分别交于点B,C.
(m≠0)的图象有公共点A(1,2).直线l⊥x轴于点N(3,0),与一次函数和反比例函数的图象分别交于点B,C.
(1)求一次函数与反比例函数的解析式;
(2)求△ABC的面积?
如图,一次函数 与反比例函数
与反比例函数 的图象交于A(1,m)、B(4,n)两点.
的图象交于A(1,m)、B(4,n)两点.
(1)求A、B两点的坐标和反比例函数的解析式;
(2)根据图象,直接写出当y >y
>y 时x的取值范围;
时x的取值范围;
(3)求△AOB的面积.
如图,一次函数 的图象与反比例函数
的图象与反比例函数 的图象交于点P,点P在第一象限.PA⊥x轴于点A,PB⊥y轴于点B.一次函数的图象分别交
的图象交于点P,点P在第一象限.PA⊥x轴于点A,PB⊥y轴于点B.一次函数的图象分别交 轴、
轴、 轴于点C、D,且S△PBD=4,
轴于点C、D,且S△PBD=4, .
.
(1)求点D的坐标;
(2)求一次函数与反比例函数的解析式;
(3)根据图象写出当 时,一次函数的值大于反比例函数的值的
时,一次函数的值大于反比例函数的值的 的取值范围.
的取值范围.
如图,一次函数 与反比例函数
与反比例函数 的图象交于
的图象交于 、
、 两点.
两点.
(1)求 、
、 两点的坐标和反比例函数的解析式;
两点的坐标和反比例函数的解析式;
(2)根据图象,直接写出当 时
时 的取值范围;
的取值范围;
(3)求 的面积.
的面积.
如图:一次函数的图象与反比例函数 的图象交于A(-2,6)和点B(4,n)
的图象交于A(-2,6)和点B(4,n)
(1)求反比例函数的解析式和B点坐标
(2)根据图象直接回答,在什么范围时,一次函数的值大于反比例函数的值.
如图,在平面直角坐标系中,O为原点,一次函数与反比例函数的图象相交于A(2,1)B(-1,-2)两点,与 轴相交于点C.
轴相交于点C.
(1)分别求反比例函数和一次函数的解析式(关系式);
(2)连接OA,求△AOC的面积.
如图,一次函数 (
( 为常数,且
为常数,且 )的图像与反比例函数
)的图像与反比例函数 的图像交于
的图像交于 ,
, 两点.
两点.
(1)求一次函数的表达式;
(2)若将直线 向下平移
向下平移 个单位长度后与反比例函数的图像有且只有一个公共点,求
个单位长度后与反比例函数的图像有且只有一个公共点,求 的值.
的值.
(年青海省西宁市)如图,一次函数 的图象与x轴交于点B,与反比例函数
的图象与x轴交于点B,与反比例函数 的图象的交点为A(﹣2,3).
的图象的交点为A(﹣2,3).
(1)求反比例函数的解析式;
(2)过点A作AC⊥x轴,垂足为C,若点P在反比例函数图象上,且△PBC的面积等于18,求P点的坐标.
试题篮
()