初中数学反比例函数与一次函数的交点问题试题

（年江西省南昌市）如图，已知直线与双曲线交于A（），B（）两点两点（A与B不重合），直线AB与x轴交于P（，0），与y轴交于点C．

（1）若A，B两点坐标分别为（1，3），（3，y₂），求点P的坐标．
（2）若，点P的坐标为（6，0），且AB=BP，求A，B两点的坐标．
（3）结合（1），（2）中的结果，猜想并用等式表示之间的关系（不要求证明）．

（年贵州省黔东南州）如图，已知反比例函数与一次函数的图象在第一象限相交于点A（1，﹣k+4）．

（1）试确定这两个函数的表达式；
（2）求出这两个函数图象的另一个交点B的坐标，并求△AOB的面积．

（年新疆、生产建设兵团）如图，在直角坐标系中，矩形OABC的顶点O与坐标原点重合，顶点A，C分别在坐标轴上，顶点B的坐标（4，2），过点D（0，3）和E（6，0）的直线分别于AB，BC交于点M，N．

（1）求直线DE的解析式和点M的坐标；
（2）若反比例函数（x＞0）的图象经过点M，求该反比函数的解析式，并通过计算判断点N是否在该函数的图象上．

（年蒙自市初中学业水平第一次模拟测试）如图，已知在平面直角坐标系中，是坐标原点，点在反比例函数的图象上，过点的直线交轴于点．

（1）求和的值；
（2）求的面积．

（年贵州省黔南州）如图，函数的图象是二、四象限的角平分线，将的图象以点O为中心旋转90°与函数的图象交于点A，再将的图象向右平移至点A，与x轴交于点B，则点B的坐标为 ．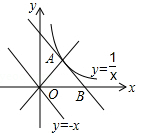

（年贵州省铜仁市）如图，在平面直角坐标系系中，直线y=k₁x+2与x轴交于点A，与y轴交于点C，与反比例函数y=在第一象限内的图象交于点B，连接B0．若S_△OBC=1，tan∠BOC=，则k₂的值是（）

A．﹣3

B．1

C．2

D．3

（年云南省昆明市）如图，直线与y轴交于点A，与反比例函数（）的图象交于点C，过点C作CB⊥x轴于点B，AO=3BO，则反比例函数的解析式为（）

A．

B．

C．

D．

（年云南省曲靖市）如图，双曲线与直线交于A、B两点，且A（﹣2，m），则点B的坐标是（）

A．（2，﹣1） B．（1，﹣2） C．（，﹣1） D．（﹣1，）

阅读理解：对于任意正实数a、b，∵(－)²≥0，∴a－2＋b≥0，∴a＋b≥2，只有当a＝b时，等号成立.
结论：在a＋b≥2（a、b均为正实数）中，若ab为定值p，则a+b≥2，只有当a＝b时，a＋b有最小值2.根据上述内容，回答下列问题：
（1）若m＞0，只有当m＝ 时，m＋有最小值 ；
若m＞0，只有当m＝ 时，2m＋有最小值 .
（2）如图，已知直线L₁：y＝x＋1与x轴交于点A，过点A的另一直线L₂与双曲线y＝（x>0）相交于点B（2，m），求直线L₂的解析式.

（3）在（2）的条件下，若点C为双曲线上任意一点，作CD∥y轴交直线L₁于点D，试求当线段CD最短时，点A、B、C、D围成的四边形面积.