初中数学二次函数的应用试题

矩形的周长等于40，则此矩形面积的最大值是　　．

某商店销售一种商品，经市场调查发现：该商品的周销售量（件是售价（元件）的一次函数，其售价、周销售量、周销售利润（元的三组对应值如表：

售价（元件）	50	60	80
周销售量（件	100	80	40
周销售利润（元	1000	1600	1600

注：周销售利润周销售量（售价进价）

（1）①求关于的函数解析式（不要求写出自变量的取值范围）；

②该商品进价是　　元件；当售价是　　元件时，周销售利润最大，最大利润是　　元．

（2）由于某种原因，该商品进价提高了元件，物价部门规定该商品售价不得超过65元件，该商店在今后的销售中，周销售量与售价仍然满足（1）中的函数关系．若周销售最大利润是1400元，求的值．

某食品厂生产一种半成品食材，成本为2元千克，每天的产量（百千克）与销售价格（元千克）满足函数关系式，从市场反馈的信息发现，该半成品食材每天的市场需求量（百千克）与销售价格（元千克）满足一次函数关系，部分数据如表：

销售价格（元千克）	2	4		10
市场需求量（百千克）	12	10		4

已知按物价部门规定销售价格不低于2元千克且不高于10元千克．

（1）直接写出与的函数关系式，并注明自变量的取值范围；

（2）当每天的产量小于或等于市场需求量时，这种半成品食材能全部售出，而当每天的产量大于市场需求量时，只能售出符合市场需求量的半成品食材，剩余的食材由于保质期短而只能废弃．

①当每天的半成品食材能全部售出时，求的取值范围；

②求厂家每天获得的利润（百元）与销售价格的函数关系式；

（3）在（2）的条件下，当为　　元千克时，利润有最大值；若要使每天的利润不低于24（百元），并尽可能地减少半成品食材的浪费，则应定为　　元千克．

某超市拟于中秋节前50天里销售某品牌月饼，其进价为18元．设第天的销售价格为（元，销售量为．该超市根据以往的销售经验得出以下的销售规律：①当时，；当时，与满足一次函数关系，且当时，；时，．②与的关系为．

（1）当时，与的关系式为　　；

（2）为多少时，当天的销售利润（元最大？最大利润为多少？

（3）若超市希望第31天到第35天的日销售利润（元随的增大而增大，则需要在当天销售价格的基础上涨元，求的取值范围．

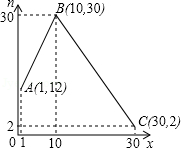
为落实“精准扶贫”精神，市农科院专家指导李大爷利用坡前空地种植优质草莓．根据场调查，在草莓上市销售的30天中，其销售价格（元公斤）与第天之间满足为正整数），销售量（公斤）与第天之间的函数关系如图所示：

如果李大爷的草莓在上市销售期间每天的维护费用为80元．

（1）求销售量与第天之间的函数关系式；

（2）求在草莓上市销售的30天中，每天的销售利润与第天之间的函数关系式；（日销售利润日销售额日维护费）

（3）求日销售利润的最大值及相应的．

"互联网 $+$ "时代，网上购物备受消费者青睐．某网店专售一款休闲裤，其成本为每条40元，当售价为每条80元时，每月可销售100条．为了吸引更多顾客，该网店采取降价措施．据市场调查反映：销售单价每降1元，则每月可多销售5条．设每条裤子的售价为 $x$ 元 $(x$ 为正整数），每月的销售量为 $y$ 条．

（1）直接写出 $y$ 与 $x$ 的函数关系式；

（2）设该网店每月获得的利润为 $w$ 元，当销售单价降低多少元时，每月获得的利润最大，最大利润是多少？

（3）该网店店主热心公益事业，决定每月从利润中捐出200元资助贫困学生．为了保证捐款后每月利润不低于4220元，且让消费者得到最大的实惠，该如何确定休闲裤的销售单价？

湘潭政府工作报告中强调，2019年着重推进乡村振兴战略，做优做响湘莲等特色农产品品牌．小亮调查了一家湘潭特产店、两种湘莲礼盒一个月的销售情况，种湘莲礼盒进价72元盒，售价120元盒，种湘莲礼盒进价40元盒，售价80元盒，这两种湘莲礼盒这个月平均每天的销售总额为2800元，平均每天的总利润为1280元．

（1）求该店平均每天销售这两种湘莲礼盒各多少盒？

（2）小亮调査发现，种湘莲礼盒售价每降3元可多卖1盒．若种湘莲礼盒的售价和销量不变，当种湘莲礼盒降价多少元盒时，这两种湘莲礼盒平均每天的总利润最大，最大是多少元？

扶贫工作小组对果农进行精准扶贫，帮助果农将一种有机生态水果拓宽了市场．与去年相比，今年这种水果的产量增加了1000千克，每千克的平均批发价比去年降低了1元，批发销售总额比去年增加了．已知去年这种水果批发销售总额为10万元．

（1）求这种水果今年每千克的平均批发价是多少元？

（2）某水果店从果农处直接批发，专营这种水果．调查发现，若每千克的平均销售价为41元，则每天可售出300千克；若每千克的平均销售价每降低3元，每天可多卖出180千克，设水果店一天的利润为元，当每千克的平均销售价为多少元时，该水果店一天的利润最大，最大利润是多少？（利润计算时，其它费用忽略不计．

如图，在正方形中，，为对角线上一动点，连接，，过点作，交直线于点．点从点出发，沿着方向以每秒的速度运动，当点与点重合时，运动停止．设的面积为，点的运动时间为秒．

（1）求证：；

（2）求与之间关系的函数表达式，并写出自变量的取值范围；

（3）求面积的最大值．

某商店购进一批成本为每件30元的商品，经调查发现，该商品每天的销售量（件与销售单价（元之间满足一次函数关系，其图象如图所示．

（1）求该商品每天的销售量与销售单价之间的函数关系式；

（2）若商店按单价不低于成本价，且不高于50元销售，则销售单价定为多少，才能使销售该商品每天获得的利润（元最大？最大利润是多少？

（3）若商店要使销售该商品每天获得的利润不低于800元，则每天的销售量最少应为多少件？

从地面竖直向上抛出一小球，小球的高度 $h$ （单位： $m)$ 与小球运动时间 $t$ （单位： $s)$ 之间的函数关系如图所示．下列结论：

①小球在空中经过的路程是 $40m$ ；

②小球抛出3秒后，速度越来越快；

③小球抛出3秒时速度为0；

④小球的高度 $h=30m$ 时， $t=1.5s$ ．

其中正确的是 $($ 　　 $)$

A．

①④

B．

①②

C．

②③④

D．

②③

攀枝花得天独厚，气候宜人，农产品资源极为丰富，其中晚熟芒果远销北上广等大城市．某水果店购进一批优质晚熟芒果，进价为10元千克，售价不低于15元千克，且不超过40元千克．根据销售情况，发现该芒果在一天内的销售量（千克）与该天的售价（元千克）之间的数量满足如下表所示的一次函数关系．

销售量（千克）		32.5	35	35.5	38
售价（元千克）		27.5	25	24.5	22

（1）某天这种芒果的售价为28元千克，求当天该芒果的销售量．

（2）设某天销售这种芒果获利元，写出与售价之间的函数关系式，如果水果店该天获利400元，那么这天芒果的售价为多少元？

在“我为祖国点赞“征文活动中，学校计划对获得一，二等奖的学生分别奖励一支钢笔，一本笔记本．已知购买2支钢笔和3个笔记本共38元，购买4支钢笔和5个笔记本共70元．

（1）钢笔、笔记本的单价分别为多少元？

（2）经与商家协商，购买钢笔超过30支时，每增加1支，单价降低0.1元；超过50支，均按购买50支的单价售，笔记本一律按原价销售．学校计划奖励一、二等奖学生共计100人，其中一等奖的人数不少于30人，且不超过60人，这次奖励一等奖学生多少人时，购买奖品总金额最少，最少为多少元？

辰星旅游度假村有甲种风格客房15间，乙种风格客房20间．按现有定价：若全部入住，一天营业额为8500元；若甲、乙两种风格客房均有10间入住，一天营业额为5000元．

（1）求甲、乙两种客房每间现有定价分别是多少元？

（2）度假村以乙种风格客房为例，市场情况调研发现：若每个房间每天按现有定价，房间会全部住满；当每个房间每天的定价每增加20元时，就会有两个房间空闲．如果游客居住房间，度假村需对每个房间每天支出80元的各种费用．当每间房间定价为多少元时，乙种风格客房每天的利润最大，最大利润是多少元？

如图，正方形中，，，点在上运动（不与、重合），过点作，交于点，则的最大值为　　．