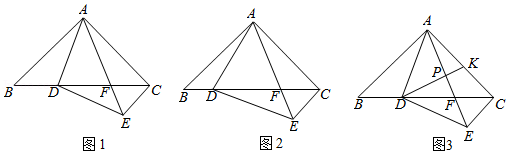
在 中, , ,点 在边 上, 且 , 交边 于点 ,连接 .
(1)特例发现:如图1,当 时,
①求证: ;
②推断: ;
(2)探究证明:如图2,当 时,请探究 的度数是否为定值,并说明理由;
(3)拓展运用:如图3,在(2)的条件下,当 时,过点 作 的垂线,交 于点 ,交 于点 ,若 ,求 的长.
如图,在 中, , , , ,点 是边 上一点,连接 ,将 沿 翻折得到 .
(1)若 , ,且 ,求 的长;
(2)连接 ,若四边形 是平行四边形,求 与 之间的关系式.

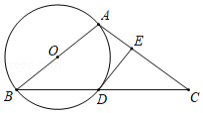
如图,在 中, ,以 为直径的 与 相交于点 ,过点 作 的切线交 于点 .
(1)求证: ;
(2)若 的半径为5, ,求 的长.
在如图所示的网格中,每个小正方形的边长为1,每个小正方形的顶点叫格点,△ ABC的三个顶点均在格点上,以点 A为圆心的  与 BC相切于点 D,分别交 AB、 AC于点 E、 F.
与 BC相切于点 D,分别交 AB、 AC于点 E、 F.
(1)求△ ABC三边的长;
(2)求图中由线段 EB、 BC、 CF及  所围成的阴影部分的面积.
所围成的阴影部分的面积.

如图,在 中, ,点 在 上,以 为半径的半圆 交 于点 ,交 于点 ,过点 作半圆 的切线 ,交 于点 .
(1)求证: ;
(2)若 , , ,求半圆 的半径长.

如图,在 中, ,以点 为圆心, 长为半径画弧,交线段 于点 ;以点 为圆心, 长为半径画弧,交线段 于点 ,连接 .
(1)若 ,求 的度数.
(2)设 , .
①线段 的长是方程 的一个根吗?说明理由.
②若 ,求 的值.
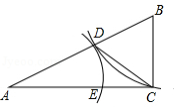
如图,在 中,点 为 的中点,弦 、 互相垂直,垂足为 , 分别与 、 相交于点 、 ,连接 、 .
(1)求证: 为 的中点.
(2)若 的半径为8, 的度数为 ,求线段 的长.
如图,已知线段 ,点 在平面直角坐标系 内.
(1)用直尺和圆规在第一象限内作出点 ,使点 到两坐标轴的距离相等,且与点 的距离等于 .(保留作图痕迹,不写作法)
(2)在(1)的条件下,若 , 点的坐标为 ,求 点的坐标.
如图1, 是 的直径,直线 与 相切于点 ,直线 与 相切于点 ,点 (异于点 在 上,点 在 上,且 ,延长 与 相交于点 ,连接 并延长交 于点 .

(1)求证: 是 的切线;
(2)求证: ;
(3)如图2,连接 并延长与 分别相交于点 、 ,连接 .若 , ,求 .
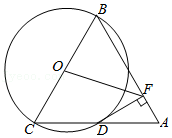
如图, 为 的直径, 为 的切线, 是 上一点,过点 的直线与 交于点 , 两点,与 交于点 ,连接 , , .
(1)求证: ;
(2)若 , ,求 的半径.

如图,Rt△ ABC中,∠ B=30°,∠ ACB=90°, CD⊥ AB交 AB于 D,以 CD为较短的直角边向△ CDB的同侧作Rt△ DEC,满足∠ E=30°,∠ DCE=90°,再用同样的方法作Rt△ FGC,∠ FCG=90°,继续用同样的方法作Rt△ HIC,∠ HCI=90°.若 AC= a,求 CI的长.

如图,在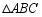 中,
中,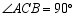 ,
,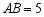 ,
,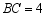 ,将
,将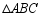 绕点
绕点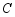 顺时针旋转
顺时针旋转 ,若点
,若点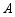 ,
,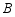 的对应点分别是点
的对应点分别是点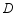 ,
, ,画出旋转后的三角形,并求点
,画出旋转后的三角形,并求点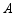 与点
与点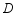 之间的距离.(不要求尺规作图)
之间的距离.(不要求尺规作图)
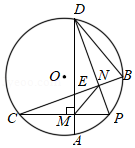
如图,以等边三角形 的 边为直径画圆,交 于点 , 于点 ,连接 ,且 .
(1)求证: 是 的切线;
(2)求线段 的长度.
问题呈现
如图1,在边长为1的正方形网格中,连接格点 , 和 , , 和 相交于点 ,求 的值.
方法归纳
求一个锐角的三角函数值,我们往往需要找出(或构造出)一个直角三角形.观察发现问题中 不在直角三角形中,我们常常利用网格画平行线等方法解决此类问题,比如连接格点 , ,可得 ,则 ,连接 ,那么 就变换到 中.
问题解决
(1)直接写出图1中 的值为 2 ;
(2)如图2,在边长为1的正方形网格中, 与 相交于点 ,求 的值;
思维拓展
(3)如图3, , ,点 在 上,且 ,延长 到 ,使 ,连接 交 的延长线于点 ,用上述方法构造网格求 的度数.

试题篮
()