初中数学菱形的判定试题

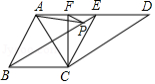
如图，在四边形中，，，点为的中点，点为的中点，，连接、、．

（1）判断四边形的形状，并说明理由；

（2）如果，，点为上的动点，求的周长的最小值．

如图1，在矩形纸片 $\mathit{ABCD}$中， $\mathit{AB}=3\mathit{cm}$， $\mathit{AD}=5\mathit{cm}$，折叠纸片使 $B$点落在边 $\mathit{AD}$上的 $E$处，折痕为 $\mathit{PQ}$，过点 $E$作 $\mathit{EF}//\mathit{AB}$交 $\mathit{PQ}$于 $F$，连接 $\mathit{BF}$．

（1）求证：四边形 $\mathit{BFEP}$为菱形；

（2）当点 $E$在 $\mathit{AD}$边上移动时，折痕的端点 $P$、 $Q$也随之移动；

①当点 $Q$与点 $C$重合时（如图 $2)$，求菱形 $\mathit{BFEP}$的边长；

②若限定 $P$、 $Q$分别在边 $\mathit{BA}$、 $\mathit{BC}$上移动，求出点 $E$在边 $\mathit{AD}$上移动的最大距离．

如图， $\mathit{\Delta ABC}\cong \mathit{\Delta ABD}$，点 $E$在边 $\mathit{AB}$上， $\mathit{CE}//\mathit{BD}$，连接 $\mathit{DE}$．求证：

（1） $\angle \mathit{CEB}=\angle \mathit{CBE}$；

（2）四边形 $\mathit{BCED}$是菱形．

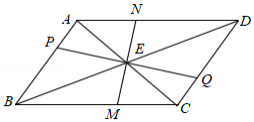
如图，过 $▱\mathit{ABCD}$对角线 $\mathit{AC}$与 $\mathit{BD}$的交点 $E$作两条互相垂直的直线，分别交边 $\mathit{AB}$、 $\mathit{BC}$、 $\mathit{CD}$、 $\mathit{DA}$于点 $P$、 $M$、 $Q$、 $N$．

（1）求证： $\mathit{\Delta PBE}\cong \mathit{\Delta QDE}$；

（2）顺次连接点 $P$、 $M$、 $Q$、 $N$，求证：四边形 $\mathit{PMQN}$是菱形．

综合与实践

动手操作：

第一步：如图1，正方形纸片沿对角线所在的直线折叠，展开铺平．在沿过点的直线折叠，使点，点都落在对角线上．此时，点与点重合，记为点，且点，点，点三点在同一条直线上，折痕分别为，．如图2．

第二步：再沿所在的直线折叠，与重合，得到图3．

第三步：在图3的基础上继续折叠，使点与点重合，如图4，展开铺平，连接，，，．如图5，图中的虚线为折痕．

问题解决：

（1）在图5中，的度数是　　，的值是　　．

（2）在图5中，请判断四边形的形状，并说明理由；

（3）在不增加字母的条件下，请你以图中5中的字母表示的点为顶点，动手画出一个菱形（正方形除外），并写出这个菱形：　　．

如图， $\mathit{AE}//\mathit{BF}$， $\mathit{AC}$平分 $\angle \mathit{BAE}$，且交 $\mathit{BF}$于点 $C$， $\mathit{BD}$平分 $\angle \mathit{ABF}$，且交 $\mathit{AE}$于点 $D$， $\mathit{AC}$与 $\mathit{BD}$相交于点 $O$，连接 $\mathit{CD}$

（1）求 $\angle \mathit{AOD}$的度数；

（2）求证：四边形 $\mathit{ABCD}$是菱形．

如图，由10根完全相同的小棒拼接而成，请你再添2根与前面完全相同的小棒，拼接后的图形恰好有3个菱形的方法共有 $($ 　　 $)$

A．

3种

B．

4种

C．

5种

D．

6种

如图， $D$ 、 $E$ 、 $F$ 分别是 $\mathit{\Delta ABC}$ 各边的中点，连接 $\mathit{DE}$ 、 $\mathit{EF}$ 、 $\mathit{AE}$ ．

（1）求证：四边形 $\mathit{ADEF}$ 为平行四边形；

（2）加上条件 　　后，能使得四边形 $\mathit{ADEF}$ 为菱形，请从① $\angle \mathit{BAC}=90°$ ；② $\mathit{AE}$ 平分 $\angle \mathit{BAC}$ ；③ $\mathit{AB}=\mathit{AC}$ 这三个条件中选择1个条件填空（写序号），并加以证明．

如图①，在中，，过上一点作交于点，以为顶点，为一边，作，另一边交于点．

（1）求证：四边形为平行四边形；

（2）当点为中点时，的形状为　　；

（3）延长图①中的到点，使，连接，，，得到图②，若，判断四边形的形状，并说明理由．

如图， $\mathit{\Delta ABC}$ 内接于圆 $O$ ，且 $\mathit{AB}=\mathit{AC}$ ，延长 $\mathit{BC}$ 到点 $D$ ，使 $\mathit{CD}=\mathit{CA}$ ，连接 $\mathit{AD}$ 交圆 $O$ 于点 $E$ ．

（1）求证： $\mathit{\Delta ABE}\cong \mathit{\Delta CDE}$ ；

（2）填空：

①当 $\angle \mathit{ABC}$ 的度数为 　　时，四边形 $\mathit{AOCE}$ 是菱形．

②若 $\mathit{AE}=\sqrt{3}$ ， $\mathit{AB}=2\sqrt{2}$ ，则 $\mathit{DE}$ 的长为 　　．

如图，在四边形 $\mathit{ABCD}$中， $\mathit{AC}$平分 $\angle \mathit{BCD}$， $\mathit{AC}\perp \mathit{AB}$， $E$是 $\mathit{BC}$的中点， $\mathit{AD}\perp \mathit{AE}$．

（1）求证： $A{C}^2=\mathit{CD}·\mathit{BC}$；

（2）过 $E$作 $\mathit{EG}\perp \mathit{AB}$，并延长 $\mathit{EG}$至点 $K$，使 $\mathit{EK}=\mathit{EB}$．

①若点 $H$是点 $D$关于 $\mathit{AC}$的对称点，点 $F$为 $\mathit{AC}$的中点，求证： $\mathit{FH}\perp \mathit{GH}$；

②若 $\angle B=30°$，求证：四边形 $\mathit{AKEC}$是菱形．

如图，在 $▱\mathit{ABCD}$中，对角线 $\mathit{AC}$与 $\mathit{BD}$相交于点 $O$，过点 $O$的直线 $\mathit{EF}$与 $\mathit{BA}$、 $\mathit{DC}$的延长线分别交于点 $E$、 $F$．

（1）求证： $\mathit{AE}=\mathit{CF}$；

（2）请再添加一个条件，使四边形 $\mathit{BFDE}$是菱形，并说明理由．

如图，点 $O$为矩形 $\mathit{ABCD}$的对称中心，点 $E$从点 $A$出发沿 $\mathit{AB}$向点 $B$运动，移动到点 $B$停止，延长 $\mathit{EO}$交 $\mathit{CD}$于点 $F$，则四边形 $\mathit{AECF}$形状的变化依次为 $($　　 $)$

A．平行四边形 $\to$正方形 $\to$平行四边形 $\to$矩形

B．平行四边形 $\to$菱形 $\to$平行四边形 $\to$矩形

C．平行四边形 $\to$正方形 $\to$菱形 $\to$矩形

D．平行四边形 $\to$菱形 $\to$正方形 $\to$矩形

如图，在 $▱\mathit{ABCD}$中， $E$， $F$分别是 $\mathit{AD}$， $\mathit{BC}$上的点，且 $\mathit{DE}=\mathit{BF}$， $\mathit{AC}\perp \mathit{EF}$．求证：四边形 $\mathit{AECF}$是菱形．

如图，四边形 $\mathit{ABCD}$ 的两条对角线相交于点 $O$ ，且互相平分．添加下列条件，仍不能判定四边形 $\mathit{ABCD}$ 为菱形的是 $($ 　　 $)$

A．

$\mathit{AC}\perp \mathit{BD}$

B．

$\mathit{AB}=\mathit{AD}$

C．

$\mathit{AC}=\mathit{BD}$

D．

$\angle \mathit{ABD}=\angle \mathit{CBD}$