初中数学菱形的判定试题

【再现】如图①，在中，点，分别是，的中点，可以得到：，且．（不需要证明）

【探究】如图②，在四边形中，点，，，分别是，，，的中点，判断四边形的形状，并加以证明．

【应用】在（1）【探究】的条件下，四边形中，满足什么条件时，四边形是菱形？你添加的条件是：　　．（只添加一个条件）

（2）如图③，在四边形中，点，，，分别是，，，的中点，对角线，相交于点．若，四边形面积为5，则阴影部分图形的面积和为　　．

在 $\mathit{\Delta ABC}$ 中， $M$ 是 $\mathit{AC}$ 边上的一点，连接 $\mathit{BM}$ ．将 $\mathit{\Delta ABC}$ 沿 $\mathit{AC}$ 翻折，使点 $B$ 落在点 $D$ 处，当 $\mathit{DM}//\mathit{AB}$ 时，求证：四边形 $\mathit{ABMD}$ 是菱形．

如图，△BAD是由△BEC在平面内绕点B旋转60°而得，且AB⊥BC，BE=CE，连接DE．

（1）求证：△BDE≌△BCE；
（2）试判断四边形ABED的形状，并说明理由．

如图，已知四边形 $\mathit{ABCD}$是平行四边形，点 $E$， $F$分别是 $\mathit{AB}$， $\mathit{BC}$上的点， $\mathit{AE}=\mathit{CF}$，并且 $\angle \mathit{AED}=\angle \mathit{CFD}$．

求证：（1） $\mathit{\Delta AED}\cong \mathit{\Delta CFD}$；

（2）四边形 $\mathit{ABCD}$是菱形．

如图， $▱\mathit{ABCD}$的对角线 $\mathit{AC}$， $\mathit{BD}$相交于点 $O$，请添加一个条件：　　，使 $▱\mathit{ABCD}$是菱形．

如图，在 $▱\mathit{ABCD}$中，对角线 $\mathit{AC}$与 $\mathit{BD}$相交于点 $O$，过点 $O$的直线 $\mathit{EF}$与 $\mathit{BA}$、 $\mathit{DC}$的延长线分别交于点 $E$、 $F$．

（1）求证： $\mathit{AE}=\mathit{CF}$；

（2）请再添加一个条件，使四边形 $\mathit{BFDE}$是菱形，并说明理由．

如图，点 $O$为矩形 $\mathit{ABCD}$的对称中心，点 $E$从点 $A$出发沿 $\mathit{AB}$向点 $B$运动，移动到点 $B$停止，延长 $\mathit{EO}$交 $\mathit{CD}$于点 $F$，则四边形 $\mathit{AECF}$形状的变化依次为 $($　　 $)$

A．平行四边形 $\to$正方形 $\to$平行四边形 $\to$矩形

B．平行四边形 $\to$菱形 $\to$平行四边形 $\to$矩形

C．平行四边形 $\to$正方形 $\to$菱形 $\to$矩形

D．平行四边形 $\to$菱形 $\to$正方形 $\to$矩形

如图，在 $▱\mathit{ABCD}$中， $E$， $F$分别是 $\mathit{AD}$， $\mathit{BC}$上的点，且 $\mathit{DE}=\mathit{BF}$， $\mathit{AC}\perp \mathit{EF}$．求证：四边形 $\mathit{AECF}$是菱形．

如图，四边形 $\mathit{ABCD}$ 的两条对角线相交于点 $O$ ，且互相平分．添加下列条件，仍不能判定四边形 $\mathit{ABCD}$ 为菱形的是 $($ 　　 $)$

A．

$\mathit{AC}\perp \mathit{BD}$

B．

$\mathit{AB}=\mathit{AD}$

C．

$\mathit{AC}=\mathit{BD}$

D．

$\angle \mathit{ABD}=\angle \mathit{CBD}$

如图，在边长为1个单位长度的小正方形组成的的网格中，给出了以格点（网格线的交点）为端点的线段．

（1）将线段向右平移5个单位，再向上平移3个单位得到线段，请画出线段．

（2）以线段为一边，作一个菱形，且点，也为格点．（作出一个菱形即可）

如图①，在 $\text{Rt}\Delta \text{ABC}$ 中， $\angle \mathit{ACB}=90°$ ， $\angle A=60°$ ， $\mathit{CD}$ 是斜边 $\mathit{AB}$ 上的中线，点 $E$ 为射线 $\mathit{BC}$ 上一点，将 $\mathit{\Delta BDE}$ 沿 $\mathit{DE}$ 折叠，点 $B$ 的对应点为点 $F$ ．

（1）若 $\mathit{AB}=a$ ．直接写出 $\mathit{CD}$ 的长（用含 $a$ 的代数式表示）；

（2）若 $\mathit{DF}\perp \mathit{BC}$ ，垂足为 $G$ ，点 $F$ 与点 $D$ 在直线 $\mathit{CE}$ 的异侧，连接 $\mathit{CF}$ ，如②，判断四边形 $\mathit{ADFC}$ 的形状，并说明理由；

（3）若 $\mathit{DF}\perp \mathit{AB}$ ，直接写出 $\angle \mathit{BDE}$ 的度数．

如图，在矩形 $\mathit{ABCD}$中， $\mathit{AC}$， $\mathit{BD}$相交于点 $O$，过点 $B$作 $\mathit{BF}\perp \mathit{AC}$于点 $M$，交 $\mathit{CD}$于点 $F$，过点 $D$作 $\mathit{DE}//\mathit{BF}$交 $\mathit{AC}$于点 $N$．交 $\mathit{AB}$于点 $E$，连接 $\mathit{FN}$， $\mathit{EM}$．有下列结论：①四边形 $\mathit{NEMF}$为平行四边形；② $D{N}^2=\mathit{MC}\cdot \mathit{NC}$；③ $\mathit{\Delta DNF}$为等边三角形；④当 $\mathit{AO}=\mathit{AD}$时，四边形 $\mathit{DEBF}$是菱形．其中，正确结论的序号 　　．

如图， $\mathit{\Delta ABC}$ 是边长为1的等边三角形， $D$ 、 $E$ 为线段 $\mathit{AC}$ 上两动点，且 $\angle \mathit{DBE}=30°$ ，过点 $D$ 、 $E$ 分别作 $\mathit{AB}$ 、 $\mathit{BC}$ 的平行线相交于点 $F$ ，分别交 $\mathit{BC}$ 、 $\mathit{AB}$ 于点 $H$ 、 $G$ ．现有以下结论： $S_{\mathit{\Delta ABC}}=\frac{\sqrt{3}}{4}$ ；②当点 $D$ 与点 $C$ 重合时， $\mathit{FH}=\frac{1}{2}$ ；③ $\mathit{AE}+\mathit{CD}=\sqrt{3}\mathit{DE}$ ；④当 $\mathit{AE}=\mathit{CD}$ 时，四边形 $\mathit{BHFG}$ 为菱形，其中正确结论为 $($ 　　 $)$

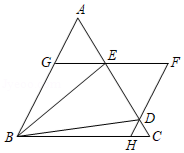
A．

①②③

B．

①②④

C．

①②③④

D．

②③④

如图， $\text{Rt}\Delta \text{OAB}$的直角边 $\mathit{OA}$在 $x$轴上，顶点 $B$的坐标为 $(6,8)$，直线 $\mathit{CD}$交 $\mathit{AB}$于点 $D(6,3)$，交 $x$轴于点 $C(12,0)$．

（1）求直线 $\mathit{CD}$的函数表达式；

（2）动点 $P$在 $x$轴上从点 $(-10,0)$出发，以每秒1个单位的速度向 $x$轴正方向运动，过点 $P$作直线 $l$垂直于 $x$轴，设运动时间为 $t$．

①点 $P$在运动过程中，是否存在某个位置，使得 $\angle \mathit{PDA}=\angle B$，若存在，请求出点 $P$的坐标；若不存在，请说明理由；

②请探索当 $t$为何值时，在直线 $l$上存在点 $M$，在直线 $\mathit{CD}$上存在点 $Q$，使得以 $\mathit{OB}$为一边， $O$， $B$， $M$， $Q$为顶点的四边形为菱形，并求出此时 $t$的值．

如图1，在矩形中，为边上一点，．将沿翻折得到△，的延长线交边于点，过点作交于点．

（1）求证：；

（2）请判断四边形的形状，并说明理由；

（3）如图2，连接，分别交，于点，．若，求的值．