如图,在平面直角坐标系中,矩形 的对角线 的中点与坐标原点重合,点 是 轴上一点,连接 .若 平分 ,反比例函数 的图象经过 上的两点 , ,且 , 的面积为18,则 的值为

A.6B.12C.18D.24
如图,一直线与两坐标轴的正半轴分别交于 , 两点, 是线段 上任意一点(不包括端点),过 分别作两坐标轴的垂线与两坐标轴围成的矩形的周长为10,则该直线的函数表达式是
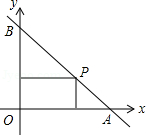
A. B. C. D.
在矩形纸片 中, , , 是边 上的点,将纸片沿 折叠,使点 落在点 处,连接 ,当 为直角三角形时, 的长为 .
如图,有一张长方形纸片 , , ,点 为 上一点,将纸片沿 折叠, 的对应边 恰好经过点 ,则线段 的长为 .

如图,矩形 的边 在 轴上,点 在第二象限,点 在第一象限, , ,将矩形 绕点 旋转,使点 落在 轴上,则点 对应点的坐标是

A. , B.
C. 或 D. , 或
如图,矩形 中, , ,点 、 分别在 、 上,且 .
(1)求证:四边形 是菱形;
(2)求线段 的长.

如图,已知 是矩形 的对角线.
(1)用直尺和圆规作线段 的垂直平分线,分别交 、 于 、 (保留作图痕迹,不写作法和证明).
(2)连接 , ,问四边形 是什么四边形?请说明理由.

如图, 在射线 上顺次取两点 , ,使 ,以 为边作矩形 , ,将射线 绕点 沿逆时针方向旋转, 旋转角记为 (其 中 ,旋转后记作射线 ,射线 分别交矩形 的边 , 于点 , . 若 , ,则下列函数图象中, 能反映 与 之间关系的是

A . B .
B .
C . D .
D .
如图,在矩形 中, , ,点 为 的中点,将 沿 折叠,使点 落在矩形内点 处,连接 ,则 的长为

A. B. C. D.
问题提出:如何将边长为 ,且 为整数)的正方形分割为一些 或 的矩形( 的矩形指边长分别为 , 的矩形)?
问题探究:我们先从简单的问题开始研究解决,再把复杂问题转化为已解决的问题.
探究一:
如图①,当 时,可将正方形分割为五个 的矩形.
如图②,当 时,可将正方形分割为六个 的矩形.
如图③,当 时,可将正方形分割为五个 的矩形和四个 的矩形
如图④,当 时,可将正方形分割为八个 的矩形和四个 的矩形
如图⑤,当 时,可将正方形分割为九个 的矩形和六个 的矩形

探究二:
当 ,11,12,13,14时,分别将正方形按下列方式分割:

所以,当 ,11,12,13,14时,均可将正方形分割为一个 的正方形、一个 的正方形和两个 的矩形.显然, 的正方形和 的矩形均可分割为 的矩形,而 的正方形是边长分别为5,6,7,8,9的正方形,用探究一的方法可分割为一些 或 的矩形.
探究三:
当 ,16,17,18,19时,分别将正方形按下列方式分割:

请按照上面的方法,分别画出边长为18,19的正方形分割示意图.
所以,当 ,16,17,18,19时,均可将正方形分割为一个 的正方形、一个 的正方形和两个 的矩形.显然, 的正方形和 的矩形均可分割为 的矩形,而 的正方形又是边长分别为5,6,7,8,9的正方形,用探究一的方法可分割为一些 或 的矩形.
问题解决:如何将边长为 ,且 为整数)的正方形分割为一些 或 的矩形?请按照上面的方法画出分割示意图,并加以说明.
实际应用:如何将边长为61的正方形分割为一些 或 的矩形?(只需按照探究三的方法画出分割示意图即可)
试题篮
()