初中数学圆内接四边形的性质试题

正方形A₁B₁C₁O，A₂B₂C₂C₁，A₃B₃C₃C₂，…按如图的方式放置．点A₁，A₂，A₃，…和点C₁，C₂，C₃，…分别在直线y=x+1和x轴上，则点B₆的坐标是            ．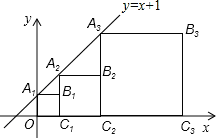

如图，分别以直角三角形的三边向外作正方形，则正方形B的面积为             ．

如图是一个小正方形的展开图，把展开图折叠成小正方形后，相对两个面上的数字之和的最大值是（）

A．11

B．9

C．7

D．5

如图，正方形ABCD的边长为，E，F分别是AB，BC的中点，AF与DE，DB分别交于点M，N，则△DMN的面积=        ．

【试题背景】已知:l ∥∥∥k，平行线l与、与、与k之间的距离分别为₁、₂、₃，且₁ =₃ = 1，₂ =" 2" ．我们把四个顶点分别在l、、、k这四条平行线上的四边形称为“格线四边形”．
【探究1】（1）如图1，正方形为“格线四边形”，于点,的反向延长线交直线k于点． 求正方形的边长．
【探究2】（2）矩形为“格线四边形”，其长 ：宽 =" 2" ：1 ，则矩形的宽为     ．（直接写出结果即可）
【探究3】（3）如图2，菱形为“格线四边形”且∠=60°，△是等边三角形，于点， ∠=90°，直线分别交直线l、k于点、． 求证：．
【拓 展】（4）如图3，l ∥k，等边三角形的顶点、分别落在直线l、k上，于点，且="4" ，∠=90°，直线分别交直线l、k于点、，点、分别是线段、上的动点，且始终保持=，于点．
猜想：在什么范围内，∥？直接写出结论。

如图，在菱形ABCD中，∠ABC=60°，BC=1cm，以DC为边在菱形的外部作正三角形CDE，连接AE，则AE=       cm．

如图，线段AC是矩形ABCD的对角线，

（1）请你作出线段AC的垂直平分线，交AC于点O，交AB于点E，交DC于点F（保留作图痕迹，不写作法）
（2）求证：AE=AF．

如图，□ABCD中，对角线AC、BD交于点O，点E是BC的中点．若OE=4，则CD的长为      ．

 

如图中，由一个直角三角形和两个正方形组成，如果大正方形的面积为41，AB=5，则小正方形的面积为____________．

已知：如图，在四边形ABCD中，AB∥CD，E，F为对角线AC上两点，且AE=CF，DF∥BE．

求证：四边形ABCD为平行四边形．

如图，在正方形ABCD中，点F为CD上一点，BF与AC交于点E．若∠CBF=20°，则∠AED等于     度．

如图，菱形ABCD的对角线的长分别为2和5，P是对角线AC上任一点（点P不与点A、C重合）且PE∥BC交AB于E，PF∥CD交AD于F，则阴影部分的面积是（ ）

A．2            B．           C．3              D．

如图1，点E为正方形ABCD的边AB上一点，EF⊥EC，且EF=EC，连接AF．
（1）求∠FAD的度数；
（2）如图2，连接FC交BD于M，求证：AD=AF+2DM；
（3）如图2，连接FC交BD于M，交AD于N．若AF=，AN=10，则BM的长为              ．

把矩形ABCD沿着CE折叠，使得点F落在AD上，若AB＝8，BC＝10，则折痕线CE＝_________．

如图所示，矩形ABCD中，AB=4，BC=，点E是折线ADC上的一个动点（点E与点A不重合），点P是点A关于BE的对称点．在点E运动的过程中，使△PCB为等腰三角形的点E的位置共有（   ）．

A．2个

B．3个

C．4个

D．5个