在□ABCD中,如果∠A+∠C=140°,那么∠C等于( ).
| A.20° | B.40° | C.60° | D.70° |
如图,菱形ABCD的对角线AC,BD相交于点O,点E,F分别是边AB,AD的中点.
(1)请判断△OEF的形状,并证明你的结论;
(2)若AB=13,AC=10,请求出线段EF的长.
如图,在菱形ABCD中,对角线AC、BD相交于点O,下列结论:①AC⊥BD;②OA=OB;③∠ADB=∠CDB;④△ABC是等边三角形,其中一定成立的是( )
A.①② B.③④ C.②③ D.①③
求证:平行四边形的对角线互相平分(要求:根据题意先画出图形并写出已知、求证、再写出证明过程).
如图,已知AB=AC=AD,∠CBD=2∠BDC,∠BAC=44°,则∠CAD的度数为( )
| A.68° | B.88° | C.90° | D.112° |
在平行四边形ABCD中,将△BCD沿BD翻折,使点C落在点E处,BE和AD相交于点O,求证:OA=OE.
如图,已知E、F、G、H分别为菱形ABCD四边的中点,AB=6cm,∠ABC=60°,则四边形EFGH的面积为 cm2.
若矩形ABCD的两邻边长分别为一元二次方程 的两个实数根,则矩形ABCD的对角线长为 .
的两个实数根,则矩形ABCD的对角线长为 .
如图,将矩形
沿
折叠,使顶点
恰好落在
边的中点
上,点
落在
处,
交
于点
.若
,
,则
的长为.

四边形的外角和为m,五边形的外角和为n,则m n(填“< 或 = 或 >”号).
如图,在平行四边形ABCD中,AC与BD交于点O,点E是BC边的中点,OE=1,则AB的长是 .
如图所示,正方形ABCD的对角线AC,BD相交于点O,DE平分∠ODC交OC于点E,若AB=2,则线段OE的长为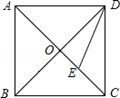
A.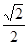 |
B.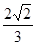 |
C.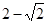 |
D.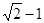 |
试题篮
()