如图,在 中, , , (圆心 在 内部)经过 、 两点,交 于点 ,过点 作 的切线交 于点 .延长 交 于点 ,作 交 于点
(1)求证:四边形 是平行四边形;
(2)若 , ,求 的值.
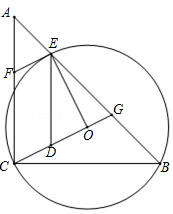
如图, 是 的直径, ,四边形 是平行四边形, 交 于点 ,连接 并延长交 的延长线于点 .
(1)求证: 是 的切线;
(2)若 , ,求图中阴影部分的面积(结果保留根号和 ).
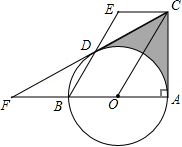
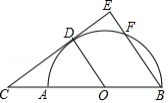
如图,四边形 ABCD中, MA= MC, MB= MD,以 AB为直径的圆 O过点 M且与 DC延长线相切于点 E.
(1)求证:四边形 ABCD是菱形;
(2)若 AB=4,求 的长(结果请保留π)

如图,在 中, ,点 在 上,以 为半径的半圆 交 于点 ,交 于点 ,过点 作半圆 的切线 ,交 于点 .
(1)求证: ;
(2)若 , , ,求半圆 的半径长.

如图,在 中, ,以 为直径的 交 于点 ,过点 作 的切线 ,交 于点 , 的反向延长线交 于点 .
(1)求证: ;
(2)若 , 的半径为10,求 的长度.

如图, 为半圆 的直径, 为半圆 上一点, 与过点 的切线垂直,垂足为 , 交半圆 于点 .
(1)求证: 平分 ;
(2)若 ,试判断以 , , , 为顶点的四边形的形状,并说明理由.

如图, 是以 为直径的半圆 的切线, 为半圆上一点, , , 的延长线相交于点 .
(1)求证: 是半圆 的切线;
(2)连接 ,求证: ;
(3)若 , ,求 的长.
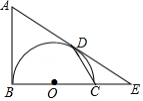
如图,在 中,以 为直径的 分别与 , 相交于点 , , ,过点 作 的切线交边 于点 .
(1)求证: ;
(2)若 的半径为5, ,求 的长(结果保留 .

如图,在平面直角坐标系中,与
轴的正半轴交于
、
两点,与
轴的正半轴相切于点
,连接
、
,已知
半径为2,
,双曲线
经过圆心
.
(1)求双曲线的解析式;
(2)求直线的解析式.

如图, AB是⊙ O的直径,弦 CD与 AB交于点 E,过点 B的切线 BP与 CD的延长线交于点 P,连接 OC, CB.
(1)求证: AE• EB= CE• ED;
(2)若⊙ O的半径为3, OE=2 BE, ,求tan∠ OBC的值及 DP的长.

已知:如图,在 中, , 与 相切于点 .求证: .小明同学的证明过程如下框:
证明:连结 , , , 又 , , . |
小明的证法是否正确?若正确,请在框内打“ ”;若错误,请写出你的证明过程.
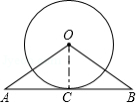
如图, 为等腰三角形, 是底边 的中点,腰 与 相切于点 , 与 相交于点 .
(1)求证: 是 的切线;
(2)若 , .求阴影部分的面积.

如图, PA为⊙ O的切线, A为切点,直线 PO交⊙ O于点 M、 N,过点 A作 PO的垂线 AB,垂足为 C,交⊙ O于点 B,延长 BO与⊙ O交于点 D,连接 AD、 BM.
(1)等式 OD 2= OC• OP成立吗?若成立,请加以证明;若不成立,请说明理由.
(2)若 AD=6,tan∠ M= ,求sin∠ D的值.

如图, 为半圆 的直径, 为 延长线上一点, 切半圆 于点 ,连接 .作 于点 ,交半圆 于点 .已知 , .
(1)求证: .
(2)求半圆 的半径 的长.
试题篮
()